フェルミ・ディラック分布関数(フェルミ分布関数)の導出には、フェルミ粒子の統計性を反映したパウリの排他原理を用いる。 すなわち、「2つの粒子は同一の状態を取らない」という性質を用いて、状態の数を求めていく。 導出するフェルミ分布関数は以下の通りである。
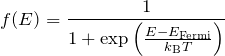
フェルミ分布関数の導出
前提:あるエネルギーにある状態の数
自由電子模型を例にすると、シュレディンガー方程式からエネルギー固有値は
![]()
で与えられていた。 このとき、同じエネルギー値をとる状態は複数通りあることがわかる。 要するに、![]() の値が同じでも、
の値が同じでも、![]() の組はいくつかある。
の組はいくつかある。
また、パウリの排他原理によると、2つの電子が同一の状態にあることはない。 スピンを ![]() で区別すると、状態
で区別すると、状態 ![]() にある電子の数は0か1(占有か非占有か)である。
にある電子の数は0か1(占有か非占有か)である。
状態の数を求める
離散化されたエネルギー準位を、エネルギーの低い順に ![]() (
(![]() ) とする。 そこで、あるエネルギー
) とする。 そこで、あるエネルギー ![]() にある状態数
にある状態数 ![]() とし、そのうち
とし、そのうち ![]() (
(![]() ) 個の状態が占有されているとする。 このとき、「占有のしかたの総数
) 個の状態が占有されているとする。 このとき、「占有のしかたの総数 ![]() 」を求めよう。
」を求めよう。
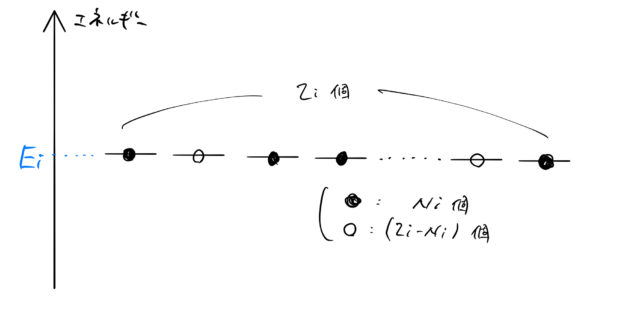
図のように、![]() を求める問題は組み合わせの問題である。 (
を求める問題は組み合わせの問題である。 (![]() 個の座席に、人を
個の座席に、人を ![]() 個だけ着席させた状態の総数)
個だけ着席させた状態の総数)
![]()
これが ![]() 番目のエネルギーにある状態数である。
番目のエネルギーにある状態数である。 ![]() についての総乗が、全てのエネルギーを考えたときの「占有のしかたの総数
についての総乗が、全てのエネルギーを考えたときの「占有のしかたの総数 ![]() 」 である。
」 である。
![]()
エントロピーを最大にする
総数 ![]() がわかるとボルツマンの原理よりエントロピー
がわかるとボルツマンの原理よりエントロピー ![]() がわかる。
がわかる。
![]()
ここで、![]() はボルツマン定数である。 熱力学によると、系が熱平衡状態にあるときエントロピー
はボルツマン定数である。 熱力学によると、系が熱平衡状態にあるときエントロピー ![]() は最大になる(非平衡であれば
は最大になる(非平衡であれば ![]() は増大する)。
は増大する)。 ![]() は単調増加関数であるため、
は単調増加関数であるため、![]() を最大化するためには
を最大化するためには ![]() (あるいは
(あるいは ![]() ) を最大化すれば良い。
) を最大化すれば良い。
* 何の条件もなかったら総数 ![]() を大きくするためには、とにかくエネルギーを大きく、座席の数 (
を大きくするためには、とにかくエネルギーを大きく、座席の数 (![]() ) を増やしまくれば良い。 そして、着席させる人の数 (
) を増やしまくれば良い。 そして、着席させる人の数 (![]() ) も増やしていけば良い。しかし、これは現実的ではない。 そこで、全エネルギーを固定し、粒子数を一定にするという条件が必要になる。 つまり、次に示すような束縛条件のもと、
) も増やしていけば良い。しかし、これは現実的ではない。 そこで、全エネルギーを固定し、粒子数を一定にするという条件が必要になる。 つまり、次に示すような束縛条件のもと、![]() を最大化していく。
を最大化していく。
** ![]() が一定のとき、
が一定のとき、![]() を
を ![]() の関数とみると上に凸の関数になる。 たとえば、6個の座席に対して、
の関数とみると上に凸の関数になる。 たとえば、6個の座席に対して、![]() として
として ![]() を計算してみると良い(
を計算してみると良い(![]() が一番大きい)。
が一番大きい)。
ラグランジュの未定乗数法を用いる
全粒子数 ![]() 一定、全エネルギー
一定、全エネルギー ![]() 一定の条件
一定の条件
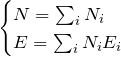
を課して、![]() を最大化する。 そのためにラグランジュの未定乗数法で求めていく。
を最大化する。 そのためにラグランジュの未定乗数法で求めていく。
2つのラグランジュの未定乗数を ![]() と置いて、
と置いて、
![]()
を最大にする。
![]()
![]() に関して上に凸の関数であるため、この条件で最大値を求めることができる。
に関して上に凸の関数であるため、この条件で最大値を求めることができる。
ここで、スターリングの公式を用いて ![]() を近似しておく。
を近似しておく。
スターリングの公式は以下の通りである。![]() が十分大きい時、
が十分大きい時、
![]()
これを用いて ![]() を簡単にする。
を簡単にする。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \ln W&=&\ln \left[\Pi_i \frac{Z_i!}{(Z_i - N_i)!(N_i)!}\right]\\ &=&\sum_i \ln\left[\frac{Z_i!}{(Z_i - N_i)!(N_i)!}\right]\\ &\textcolor{red}{\simeq}&\sum_i\left[Z_i\ln Z_i \cancel{-Z_i} - (Z_i-N_i)\ln (Z_i-N_i) + \cancel{(Z_i-N_i)} -N_i \ln N_i + \cancel{N_i}\right]\\ &=&\sum_i\left[Z_i\ln Z_i - (Z_i-N_i)\ln (Z_i-N_i) -N_i \ln N_i\right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-53c2422bd87e7701bef0c19da6b56587_l3.png)
したがって、式(1)の偏微分は
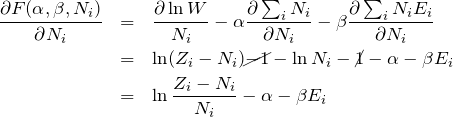
(![]() の項の偏微分の計算については補足に記載
の項の偏微分の計算については補足に記載![]() )
)
よって、
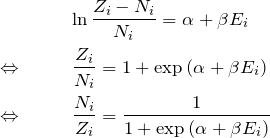
![]() を連続変数として扱えば、
を連続変数として扱えば、
![]()
補足[1]: ![]() に関する偏微分のところを簡単に書いておく。
に関する偏微分のところを簡単に書いておく。
![]()
![]()
![]()
![]()
熱力学の式から乗数を求める
熱力学で現れる関係式から、ラグランジュの未定乗数 ![]() を求める。 エントロピーを
を求める。 エントロピーを ![]() 、内部エネルギーを
、内部エネルギーを ![]() 、化学ポテンシャルを
、化学ポテンシャルを ![]() 、粒子数を
、粒子数を ![]() とすると、
とすると、
![]()
の関係がある。体積一定とすると、
![]()
である。
一方、![]() )の
)の ![]() に対する変分をゼロとして、
に対する変分をゼロとして、
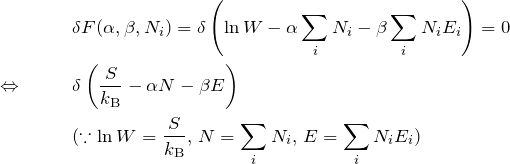
となる(![]() は一定なので消えている)。 これを
は一定なので消えている)。 これを ![]() の形に書くと、
の形に書くと、
![]()
となる。式(3)’と比較すると、
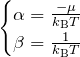
となる。
この![]() を用いて、式(2)からフェルミ分布関数がわかる。
を用いて、式(2)からフェルミ分布関数がわかる。
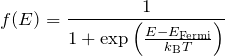
ここでは ![]() ではなく、温度に依存するフェルミエネルギー
ではなく、温度に依存するフェルミエネルギー ![]() で表している。
で表している。