ボーズ・アインシュタイン分布関数に従う粒子は、スピンが整数であるボーズ粒子である。 一方、スピンが半整数(例えばスピン1/2の電子など)のフェルミ粒子の場合はフェルミ分布関数に従い、導出にはパウリの排他原理を用いた。 ボーズ粒子とフェルミ粒子の統計性の違いが分布関数の違いを生んでいる。
ここでは、以下のボーズ・アインシュタイン分布関数を導出する。
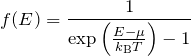
ボーズ・アインシュタイン分布関数の導出
あるエネルギー状態数
異なる状態でも同一のエネルギーになる。そのことは、自由電子のエネルギー ![]() について、
について、![]() と
と ![]() が同じエネルギーになることからわかる。 そのことはボーズ粒子の場合も同様である。
が同じエネルギーになることからわかる。 そのことはボーズ粒子の場合も同様である。
はじめに、エネルギー ![]() にある状態数
にある状態数 ![]() を求めるため、 とりうる状態を
を求めるため、 とりうる状態を ![]() として、ボーズ粒子が
として、ボーズ粒子が ![]() 個ある場合を考える。フェルミ粒子はパウリの排他原理を満たしたが、ボーズ粒子はそのような制限がないため、複数のボーズ粒子が同一の状態をとってもよい。
個ある場合を考える。フェルミ粒子はパウリの排他原理を満たしたが、ボーズ粒子はそのような制限がないため、複数のボーズ粒子が同一の状態をとってもよい。
かんたんな例として ![]() 個のボールを
個のボールを ![]() 個の袋にいれる問題を考える。 このとき、1個の袋に2個以上のボールが入っていても良い。 ボールを袋に詰める詰め方は図のように
個の袋にいれる問題を考える。 このとき、1個の袋に2個以上のボールが入っていても良い。 ボールを袋に詰める詰め方は図のように ![]() の係数を求める問題に帰着する。
の係数を求める問題に帰着する。

つまり、
![]()
を展開したときの ![]() の係数を求めることと同じである(重複組み合わせによる別の考え方はページ一番下の補足に書いた)。
の係数を求めることと同じである(重複組み合わせによる別の考え方はページ一番下の補足に書いた)。
一般化すると、
![]()
における ![]() の係数が求める
の係数が求める ![]() になる。
になる。
式(1) のカッコ内は無限等比級数(初項1, 等比 ![]() )であるため
)であるため
![]()
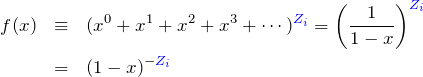
となる。
さらに ![]() を
を ![]() まわりでテイラー展開
まわりでテイラー展開![]() して
して ![]() の係数を求める。そのために、
の係数を求める。そのために、![]() の
の ![]() 階微分を求めておく。
階微分を求めておく。
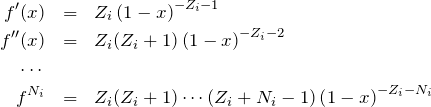
これより、![]() のテイラー展開は
のテイラー展開は
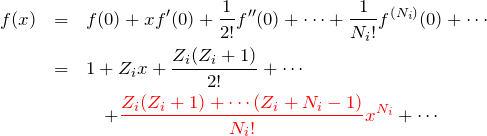
となり、![]() の係数が
の係数が
![]()
となる。(これは「考え方2」でみるように組み合わせの総数 ![]() に対応する。)
に対応する。)
* ![]() におけるテイラー展開(マクローリン展開)
におけるテイラー展開(マクローリン展開)
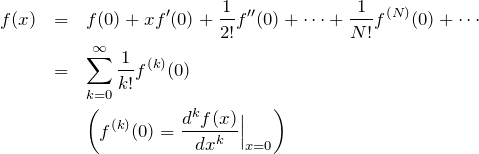
全状態の数を求める
これが ![]() 番目のエネルギー
番目のエネルギー ![]() にある状態数である。
にある状態数である。 ![]() についての総乗が、全てのエネルギーを考えたときの「占有のしかたの総数
についての総乗が、全てのエネルギーを考えたときの「占有のしかたの総数 ![]() 」 である。
」 である。
![]()
エントロピーを最大にする
総数 ![]() がわかるとボルツマンの原理よりエントロピー
がわかるとボルツマンの原理よりエントロピー ![]() がわかる。
がわかる。
![]()
ここで、![]() はボルツマン定数である。 熱力学によると、系が熱平衡状態にあるときエントロピー
はボルツマン定数である。 熱力学によると、系が熱平衡状態にあるときエントロピー ![]() は最大になる(非平衡であれば
は最大になる(非平衡であれば ![]() は増大する)。
は増大する)。 ![]() は単調増加関数であるため、
は単調増加関数であるため、![]() を最大化するためには
を最大化するためには ![]() を最大化すれば良い。 つまり、次に示すような束縛条件のもと、
を最大化すれば良い。 つまり、次に示すような束縛条件のもと、![]() を最大化していく。
を最大化していく。
ラグランジュの未定乗数法を用いる
全粒子数 ![]() 一定、全エネルギー
一定、全エネルギー ![]() 一定の条件
一定の条件
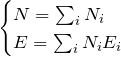
を課して、![]() を最大化する。 そのためにラグランジュの未定乗数法で求めていく。
を最大化する。 そのためにラグランジュの未定乗数法で求めていく。
2つのラグランジュの未定乗数を ![]() と置いて、
と置いて、
![]()
を最大にする。
![]()
![]() に関して上に凸の関数であるため、この条件で最大値を求めることができる。
に関して上に凸の関数であるため、この条件で最大値を求めることができる。
ここで、スターリングの公式を用いて ![]() を近似しておく。
を近似しておく。
スターリングの公式は以下の通りである。![]() が十分大きい時、
が十分大きい時、
![]()
これを用いて ![]() を簡単にする。
を簡単にする。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \ln W&=&\ln \left[\Pi_i \frac{(Z_i+N_i-1)!}{N_i!(Z_i-1)!}\right]\\ &=&\sum_i \ln\left[\frac{Z_i+N_i-1!}{N_i!(Z_i-1)!}\right]\\ &\textcolor{red}{\simeq}&\sum_i\Bigg[(Z_i+N_i-1)\ln (Z_i+N_i-1) \cancel{-(Z_i+N_i-1)}\\ &&\quad - N_i\ln N_i + \cancel{N_i} -(Z_i-1) \ln (Z_i-1) + \cancel{Z_i-1}\Bigg]\\ &=&\sum_i\Bigg[(Z_i+N_i-1)\ln (Z_i +N_i-1)\\ &&\quad - N_i\ln N_i -(Z_i-1) \ln (Z_i-1)\Bigg] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-588357b24eeeba643adb7e9e7e3f6636_l3.png)
これを ![]() で偏微分すると、
で偏微分すると、
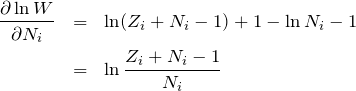
したがって、式(2)の ![]() についての偏微分は
についての偏微分は
![]()
(![]() の項の偏微分の計算については補足に記載
の項の偏微分の計算については補足に記載![]() )
)
よって、
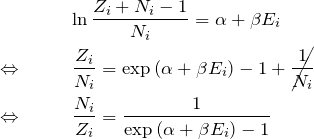
となる。途中で状態数、粒子数が多いという条件 ![]() より
より ![]() を無視した。 得られた結果は考えているエネルギー
を無視した。 得られた結果は考えているエネルギー ![]() をとる状態数
をとる状態数 ![]() に対して、ボーズ粒子が粒子数
に対して、ボーズ粒子が粒子数 ![]() だけ占有している場合の確率を表す。
だけ占有している場合の確率を表す。
![]() を連続変数として扱えば、
を連続変数として扱えば、
![]()
がボーズ・アインシュタイン分布関数となる。
![]() については熱力学の関係式から
については熱力学の関係式から
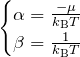
となる(参考:フェルミ分布関数の導出[熱力学の式から定数を求める])。![]() は系の化学ポテンシャルである。
は系の化学ポテンシャルである。
この![]() を用いて、式(3)からボーズ・アインシュタイン分布関数がわかる。
を用いて、式(3)からボーズ・アインシュタイン分布関数がわかる。
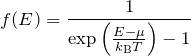
補足[1]: ![]() に関する偏微分のところを簡単に書いておく。
に関する偏微分のところを簡単に書いておく。
![]()
について、![]() における
における ![]() はダミーであるので、本当は
はダミーであるので、本当は
![]()
とすべきであった。そうすると、
![]()
であるため、
![]()
になる。
プランクの分布関数
ラグランジュの未定乗数 ![]() は粒子数一定の条件からあらわれた。 粒子数一定の条件を課さない場合は分布関数中に
は粒子数一定の条件からあらわれた。 粒子数一定の条件を課さない場合は分布関数中に ![]() はあらわれない。したがって、 ボーズ・アインシュタイン分布関数は
はあらわれない。したがって、 ボーズ・アインシュタイン分布関数は
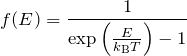
のプランクの分布関数になる。
フェルミ分布関数の形
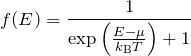
から、フェルミ分布関数は ![]() であった。 これはパウリの排他原理より、ある状態にフェルミ粒子が存在する確率が1より大きくならないことをあらわす(パウリの排他原理を反映)。
であった。 これはパウリの排他原理より、ある状態にフェルミ粒子が存在する確率が1より大きくならないことをあらわす(パウリの排他原理を反映)。
一方で、ボーズ・アインシュタイン分布関数あるいはプランクの分布関数では ![]() の分母をもつため、
の分母をもつため、![]() が1より大きくなることがある。 特に高温で
が1より大きくなることがある。 特に高温で ![]() が大きい場合は分母が0に近く(
が大きい場合は分母が0に近く(![]() が1に近く)ため、粒子数が増大する。
が1に近く)ため、粒子数が増大する。
状態数を求める考え方2
![]() 個のボールを
個のボールを ![]() 個の袋にいれる問題について別の考え方を書いておく。
これは6個のボールを3つの袋に分ける重複組合せである(この名前より意味が大切である)。
個の袋にいれる問題について別の考え方を書いておく。
これは6個のボールを3つの袋に分ける重複組合せである(この名前より意味が大切である)。
とにかく6つを3つに分けるため、6個のボールと2 (3-1) 個の仕切り棒を用意すればよい(図)。
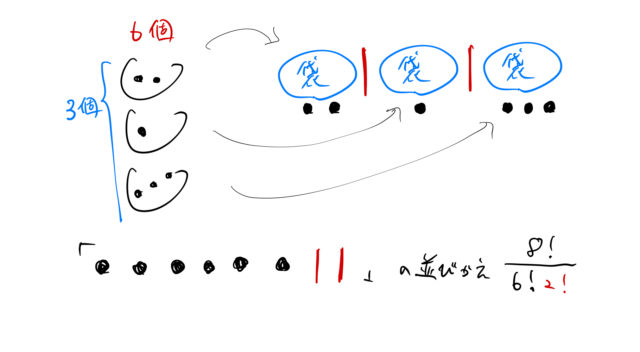
これを並び替えて
![]()
が組み合わせの総数となる。
一般化すると、![]() 個のボールと
個のボールと ![]() 個の棒の並びの総数を求めれば良い。つまり
個の棒の並びの総数を求めれば良い。つまり
![]()