ここでは以下のような同次型に似た問題を扱う。
![]()
変数変換により同次型に帰着することがわかる。(同次型がわからない・解けない方は先に「同次型の解法」で解法を習得したほうがよいだろう。) 以下の例題を使って解説していこう。
次の微分方程式を解け。
![]()
1. 同次型に帰着する方針
冒頭に示したように同次型ではないため、 変数変換により同次型に帰着させる。 どのように変数変換するか、その考え方を以下に示す。
「同次型ではない」という意味
同次型であれば、
![]()
のように、項の次数が同じであるはず。しかし、本問題では
![]()
のように定数項(0次の項)が混じっている。 したがって、整理すると
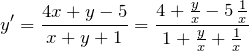
のようになる。同次型と同じ解法は使えなさそうである。
「同次型にしてしまえばよい」という発想
今、困っているのは「定数項の存在」である。 したがって、変数 ![]() を変換して定数項を消してしまえば、同次型の問題になるはず。
を変換して定数項を消してしまえば、同次型の問題になるはず。
どのように変数変換するかが大事である。 まず、分子と分母を見てみよう。これらは1次式である。
![]()
とすれば「2本の直線」の式になる。
直線における定数項の役割は「切片」である。 2直線を描いてみよう。
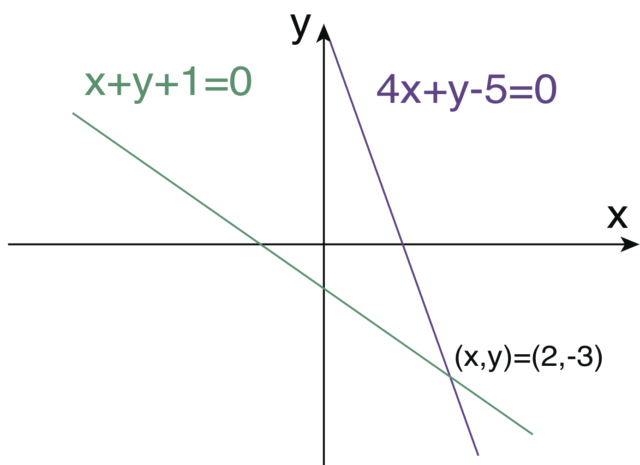
そして、いま目指していることは定数項を消すこと、 すなわち、切片が0になるような変数変換をすることである。 それも2本の直線とも!
したがって、 新たな ![]() 平面の原点が2直線の交点を通るようにすればよい。
平面の原点が2直線の交点を通るようにすればよい。
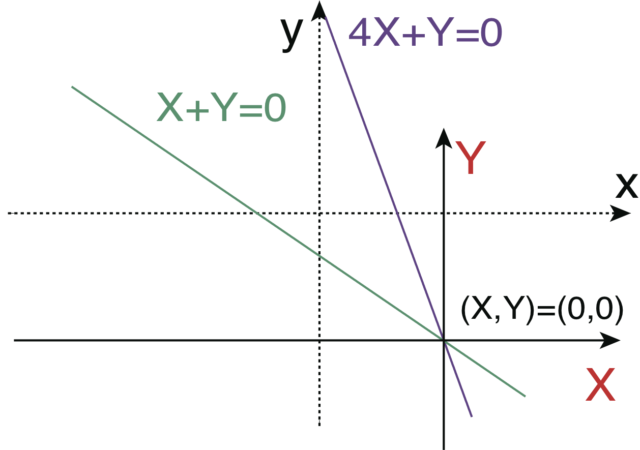
これに対応する変数変換は、
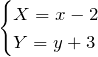
である。図から明らかなように、
![]()
となり、定数項が消えた。
次に左辺 ![]() を考える。
を考える。 ![]() は
は ![]() を
を ![]() で微分したものである。微分は傾き(変化率)に対応するものであるため、 上のような平行移動による変換では変わらない。したがって
で微分したものである。微分は傾き(変化率)に対応するものであるため、 上のような平行移動による変換では変わらない。したがって
![]()
である。
そういうわけで、![]() の変換により 微分方程式は
の変換により 微分方程式は
![]()
となり、「同次型の微分方程式」に帰着する。
解法まとめ
上の結果をまとめよう。
![]()
の同次型に似た微分方程式の解法の流れを以下に示す。
2. 例題の解答
以下、![]() などは定数である。
などは定数である。
【解答】
![]()
を変形して、
![]()
ここで、2直線
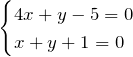
の交点は ![]() であるため、
であるため、
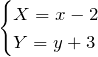
と置く。 したがって、もとの微分方程式は
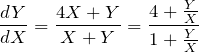
となる(変数分離型に帰着)。
![]()
と置くと
![]()
である。このとき微分方程式は、
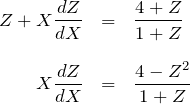
となる。
したがって、
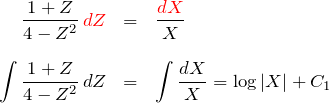
となる。
左辺は
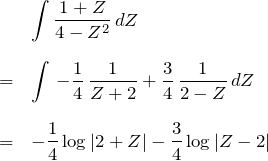
となる。
よって、
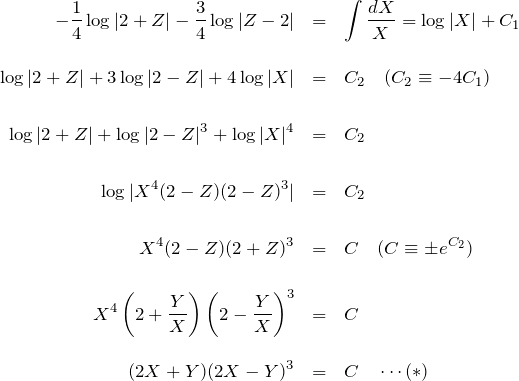
となる。
![]() に変換して、
に変換して、
![]()
となる。
* 結果(*)のチェックは、両辺を ![]() で微分してみれば良い。
で微分してみれば良い。
![]()
について、左辺は
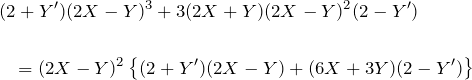
となる。したがって、
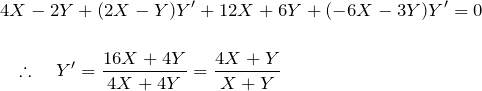
となり、もとの微分方程式を得る。
** ![]() 計算のコツ:
計算のコツ:![]() の和が多くなってくると絶対値が外しにくい。
したがって、
の和が多くなってくると絶対値が外しにくい。
したがって、![]() の中身を積の形にしてから絶対値を外すのが良いと思う。
の中身を積の形にしてから絶対値を外すのが良いと思う。
3. まとめ
2直線をイメージして交点をずらすことにより、定数項を消す。 これによって同次型に帰着させれば、微分方程式が解ける。解答の流れはこうであった。
ところで、2直線に交点がなく平行になっている場合は… たとえば、
![]()
のような場合。このタイプはここで扱った変数変換ではない解き方が必要である。