ビオ・サバール(ビオ・サヴァール)の法則をマクスウェル方程式から丁寧に導出する。そのためには、電流が作る磁場について考え、電磁気学のマクスウェル方程式の理解が必要である。ベクトル解析に慣れていないと計算につまづくかもしれない。
1. 磁場Hに関するマクスウェル方程式
真空中でのマクスウェル方程式のうち、div![]() とrot
とrot![]() に関するものを用いる。
に関するものを用いる。
![]()
これは、磁場の湧き出し(divergence, 発散)がないことを表す。つまり、磁気単極子, magnetic monopoleが存在しないことを表す(現在では存在しないことになっている。)。電荷の場合は、正電荷、負電荷による湧き出しの可能性があるので、div![]() 。いわゆる、ガウスの法則である。
。いわゆる、ガウスの法則である。
![]()
この式はアンペール・マクスウェルの式という。![]() は磁場の回転(rotation)を表す。
は磁場の回転(rotation)を表す。![]() は電流を表す。アンペールの式によると、電流
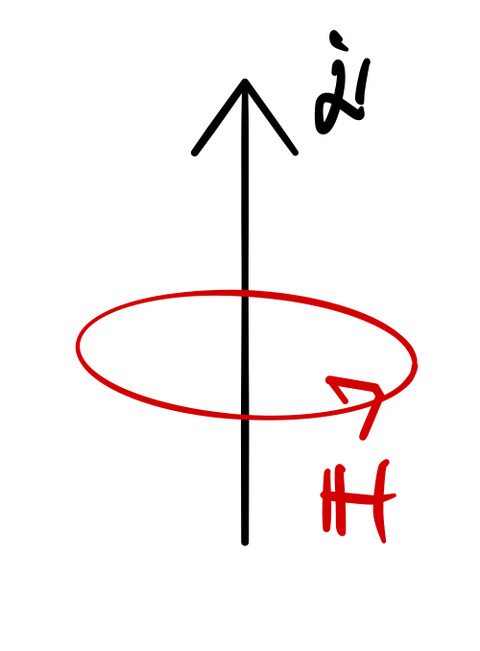
は電流を表す。アンペールの式によると、電流![]() が流れれば、図のように電流の周りに磁場が生まれる。 マクスウェルは、電場の時間変化である変位電流
が流れれば、図のように電流の周りに磁場が生まれる。 マクスウェルは、電場の時間変化である変位電流 ![]() もまた、電流と同じ役割をもつことを示した。
もまた、電流と同じ役割をもつことを示した。
2. 定常的な運動を考える
ビオ・サバールの法則に必要なのは電流であるが、それは電荷の定常的な運動によって記述できる。すなわち、それは電荷の運動の時間的な平均である。時間的な平均について考えるために、上のマクスウェル方程式の時間平均を取る。第1式については以下の通り。
![]()
![]()
である。ここで、右辺の第1項について 考える。ある時間の関数
![]()
である。時間
![]()
である。 まとめるとここまでで以下の2式を得た。
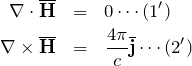
3. 新しい式を導く
(1′)について、ベクトル解析によるとdiv![]() を満たすときは、
を満たすときは、![]() とベクトルポテンシャル
とベクトルポテンシャル ![]() を用いて磁場を表すことができた。(ベクトル解析の式
を用いて磁場を表すことができた。(ベクトル解析の式 ![]() による[証明はこちらの記事]。)
による[証明はこちらの記事]。)
いま、時間平均を考えているので、
![]()
である。最終的に求めるのは磁場 ![]() であるが、この式から
であるが、この式から ![]() が分かれば、その回転
が分かれば、その回転 ![]() をとることによって
をとることによって![]() が求められる。当面の問題は
が求められる。当面の問題は ![]() を求めることである。これを、(2′)へ代入しよう。左辺は、
を求めることである。これを、(2′)へ代入しよう。左辺は、
![]()
である。ここで、以下のベクトル三重積の変形(BAC-CAB則)を用いた。「バックキャブ」などと唱えて覚えるべきベクトル解析の公式である。
![]()
(3)式の第1項に現れる
![]()
![]()
と同じ形をしている。この式の意味は、電荷(電荷密度
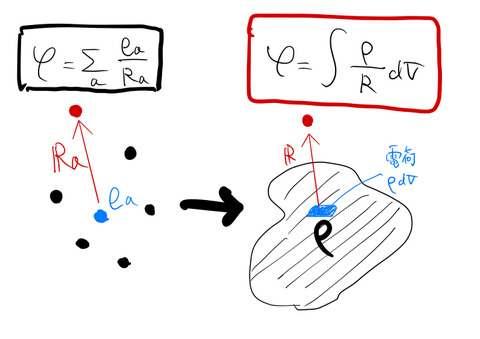
電場のポテンシャルはよく知られているように電荷からの距離 ![]() に反比例する。図(左)のように電荷が離散的であるときは、
に反比例する。図(左)のように電荷が離散的であるときは、 ![]() を用いて各電荷のポテンシャルへの寄与の総和で表される。
を用いて各電荷のポテンシャルへの寄与の総和で表される。
連続的な場を考える場合は、図(右)のように ![]() は積分記号に置き換えて、電荷密度
は積分記号に置き換えて、電荷密度 ![]() によりスカラーポテンシャル
によりスカラーポテンシャル![]() を記述する。
を記述する。
このスカラーポテンシャル ![]() と同じように、ベクトルポテンシャル
と同じように、ベクトルポテンシャル ![]() の形を作る。そうすると、ポアソン方程式 (4) の解は、
の形を作る。そうすると、ポアソン方程式 (4) の解は、
![]()
で与えられるだろう。
4. A から H がわかる
最後のステップである。式 (5)のrotation(回転)をとり、![]() を導く。
を導く。
![]()
である。右辺のrotationの
![]()
の被積分関数、
![]()
を計算する。式(7)の右辺第1項については、合成関数の微分として、
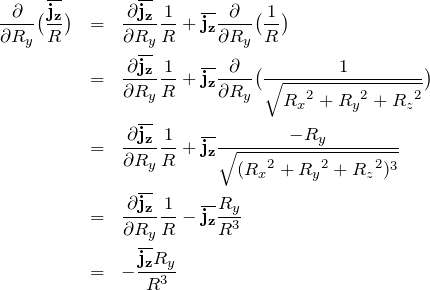
最後の行では、
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}\Bigl[ \nabla\times \bigl(\frac{\overline{\bf j}}{R}\bigr) \Bigr]_x &=&-\frac{\overline{\bf j_z} R_y}{R^{3}}-\Bigl(-\frac{\overline{\bf j_y} R_z}{R^{3}}\Bigr)\\&=&\frac{1}{R^3} \Bigl( \overline{\bf j_y} R_z - \overline{\bf j_z} R_y \Bigr)\\&=&\frac{1}{R^3} \Bigl[ \overline{\bf j} \times {\bf R}\Bigr]_x\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-b201e372069dec9a7297a4cd35c73c94_l3.png)
のようになる。
![Rendered by QuickLaTeX.com \begin{eqnarray*}\Bigl[ \nabla\times \bigl(\frac{\overline{\bf j}}{R}\bigr) \Bigr]_y =\frac{1}{R^3} \Bigl[ \overline{\bf j} \times {\bf R}\Bigr]_y\\\Bigl[ \nabla\times \bigl(\frac{\overline{\bf j}}{R}\bigr) \Bigr]_z=\frac{1}{R^3} \Bigl[ \overline{\bf j} \times {\bf R}\Bigr]_z\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-aa8407dd08e4247abad45c1e679475cc_l3.png)
であるので、式 (6)に代入して、 ビオ・サバールの法則
![]()
で表されるビオ・サバールの法則を得る。動径ベクトル ![]() は考えている体積要素
は考えている体積要素 ![]() から求めている場に向かう方向である。
から求めている場に向かう方向である。