ベクトル解析の各種の公式は、成分ごとに考えるのがわかりやすい。また、前提として、divはベクトルに作用して、スカラー量をつくることを理解しておく。(ベクトル同士の内積と同じである。)ここでは触れ無いが、実はレヴィ=チヴィタの記号を学べば、ベクトル解析のrot(rot![]() )=0などの公式は即座に導けることがわかるだろう。
)=0などの公式は即座に導けることがわかるだろう。
1. 成分ごとに計算
![]()
について、![]() 成分を計算すると、
成分を計算すると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \Bigl[\nabla\cdot(\nabla\times{\bf A})\Bigr]_x&=& \nabla_x \Bigl[ \nabla \times {\bf A} \Bigr]_x\\ &=& \nabla_x \Bigl[ \nabla_y {\bf A}_z - \nabla_z {\bf A}_y \Bigr]\\ &=& \nabla_x \nabla_y {\bf A}_z - \nabla_x \nabla_z {\bf A}_y \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-eb949a46bcc07a88089cb0551b4fd12b_l3.png)
となる。ここで、
![]()
と略記した。![]() 、
、![]() 成分も同様にして、
成分も同様にして、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \Bigl[\nabla\cdot(\nabla\times{\bf A})\Bigr]_y = \nabla_y \nabla_z {\bf A}_x - \nabla_y \nabla_x {\bf A}_z\\ \Bigl[\nabla\cdot(\nabla\times{\bf A})\Bigr]_z = \nabla_z \nabla_x {\bf A}_y - \nabla_z \nabla_y {\bf A}_x \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-a0a461d462d254caa986bbf375428b5b_l3.png)
を得る。したがって、式(*)は、
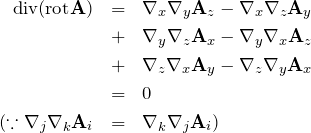
となる。![]() が証明された。
が証明された。