以下のような「ヴァンデルモンドの行列式(Vandermonde’s determinant)」 と呼ばれる特殊な行列式がある。 対照的な綺麗な形をしており、行列式の性質を使うことで証明することができる。
ヴァンデルモンドの行列式
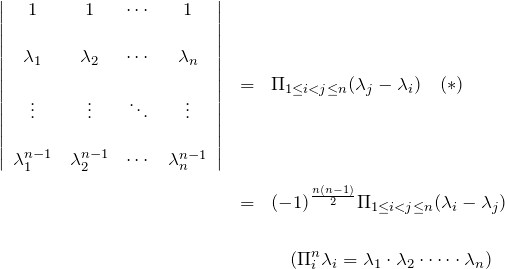
1. 証明
方針:帰納法を用いる。
【証明】
(i) ![]() のとき
のとき
![]()
より(*)は成り立つ。
(ii) ![]() のとき(*)が成り立つと仮定する。
のとき(*)が成り立つと仮定する。
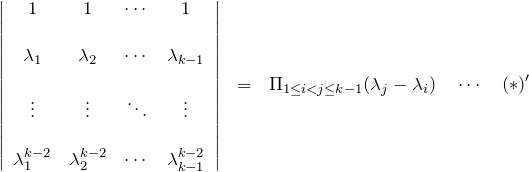
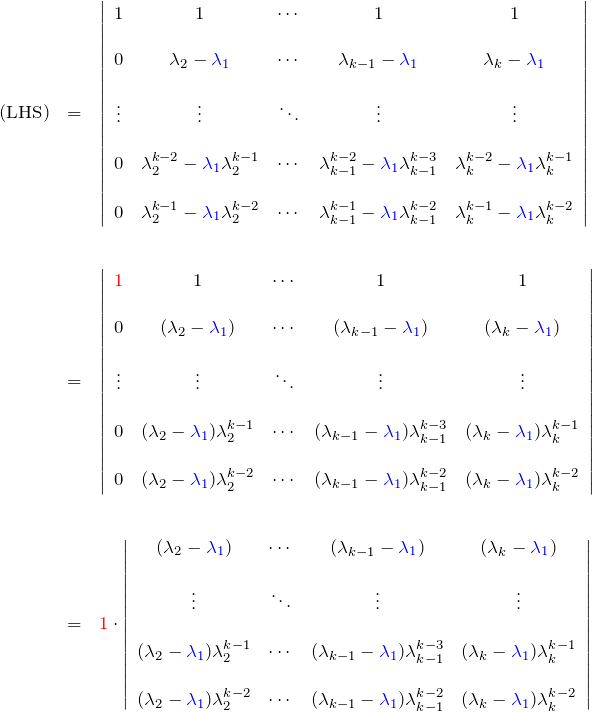
このとき、![]() に対して(*)の左辺(LHS; left-hand side)は
に対して(*)の左辺(LHS; left-hand side)は
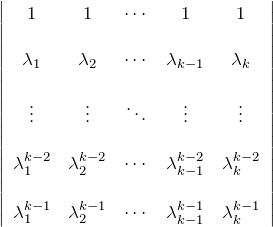
である。
ここで以下の操作をおこなう。
証明のポイント
- (n行目)-
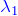 ×(n-1行目)
×(n-1行目) - (n-1行目)-
 ×(n-2行目)
×(n-2行目) - ・・・
- (2行目)-
 ×(1行目)
×(1行目)
この操作により、
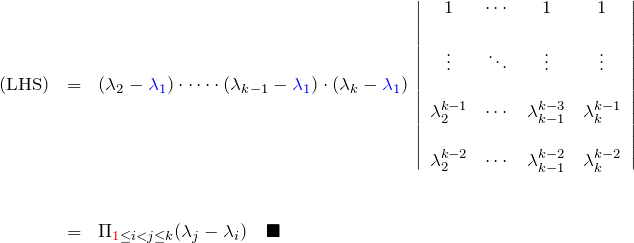
![]() は
は ![]() の
の ![]() 個ある。また、
個ある。また、![]() と入れ替えるごとに
と入れ替えるごとに ![]() の因子がつく。
の因子がつく。
したがって最後の行で ![]() と書き換えると、
と書き換えると、
![]()
となる。
以上より、ヴァンデルモンドの行列式(*)が成り立つことが示された。![]()
2. 登場場面
本サイトでは![]() 階線形微分方程式の基本解に関する「ロンスキー行列の行列式」で登場した。 そういったこともあり証明方法をここにまとめた次第。
階線形微分方程式の基本解に関する「ロンスキー行列の行列式」で登場した。 そういったこともあり証明方法をここにまとめた次第。
3. まとめ
![]() とか
とか ![]() とか分かりにくかったら
とか分かりにくかったら ![]() くらいの小さい行列で具体的に計算してみるのが良いと思います。
くらいの小さい行列で具体的に計算してみるのが良いと思います。