【微分方程式】ステュルム-リウヴィル(Sturm-Liouville)型
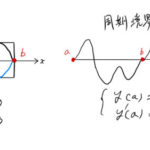
ステュルム-リウヴィル(Sturm-Liouville)型微分方程式 について見ていく。2階微分方程式であるので、解には2つの積分定数が現れる。 この微分方程式を解いて一般解を求めるのではな …
もっと読む 【微分方程式】ステュルム-リウヴィル(Sturm-Liouville)型バター猫のパラドックス

ステュルム-リウヴィル(Sturm-Liouville)型微分方程式 について見ていく。2階微分方程式であるので、解には2つの積分定数が現れる。 この微分方程式を解いて一般解を求めるのではな …
もっと読む 【微分方程式】ステュルム-リウヴィル(Sturm-Liouville)型
ルジャンドル多項式 は、ルジャンドルの微分方程式の2つ特殊解から作られる。 ルジャンドルの微分方程式は2階線形微分方程式で、 で与えられる。 そのことを詳しく見て …
もっと読む 【微分方程式】ルジャンドル多項式の導出(ルジャンドルの微分方程式)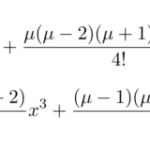
ルジャンドルの微分方程式 を解いて2つの特殊解を求める。微分方程式は まわりの級数展開により解いていく。「【微分方程式】級数解による解法(整級数)」の手法がそのまま使える。 得られる2つの …
もっと読む 【微分方程式】ルジャンドルの微分方程式/級数解による解法
ラーゲル多項式(陪多項式)、ルジャンドル多項式(陪多項式)、球面調和関数など、球対称ポテンシャル をもつ極座標表示のシュレディンガー方程式を解く過程で複雑なものがたくさん出てくる。ここではもう、2.1以降でざっくりとま …
もっと読む 【ざっくりまとめ】 極座標表示のシュレディンガー方程式 の産物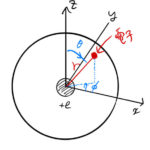
微分演算子であるルジャンドリアン の固有値問題である を解いて、固有関数を求めていく。ここで固有値は としている。 あとにわかるように、この固有関数 は球面調和関数になっている。 導入 かん …
もっと読む 球面調和関数⓪:ルジャンドリアンの固有値問題