簡単な以下の微分方程式をラプラス変換を用いて解く。
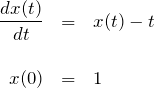
【解答】
![]() をラプラス変換した
をラプラス変換した ![]() を定義する。
を定義する。
![]()
与えられた微分方程式の両辺をラプラス変換する。![]() 世界
世界 ![]()
![]() 世界。
世界。
&=& {\mathcal L}\left[x(t)\right](s)-{\mathcal L}\left[t\right](s)\\\\ sX(s)-x(0)&=&X(s)-\frac{1}{s^2}\\\\ (s-1)X(s)&=&1-\frac{1}{s^2}\\\\ \therefore \quad X(s)&=&\frac{s^2-1}{s^2}\cdot\frac{1}{s-1}\\\\ &=& \frac{s+1}{s^2}\\\\ &=& \frac{s}{s^2}+\frac{1}{s^2}\\\\ &=& \frac{1}{s}+\frac{1}{s^2} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-64efdcfe08e8693a5f47a7e2a4afe6dc_l3.png)
これをラプラス逆変換して、
![]()
解答の過程で利用したもの
導関数 f'(x) のラプラス変換 、![]() のラプラス変換、
のラプラス変換、![]() のラプラス変換
のラプラス変換
&=&s{\mathcal L}[f(t)](s)-f(0)\\\\ {\mathcal L}[t](s)&=&\frac{1}{s^2}\\\\ {\mathcal L}[1](s)&=&\frac{1}{s} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-62ed6bb6a6cad083b4ce400179cfde35_l3.png)
ラプラス逆変換のときには、![]() と
と ![]() のラプラス変換が
のラプラス変換が ![]() 、
、![]() になることを利用した。
になることを利用した。
バター猫のパラドックス
簡単な以下の微分方程式をラプラス変換を用いて解く。
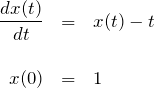
【解答】
![]() をラプラス変換した
をラプラス変換した ![]() を定義する。
を定義する。
![]()
与えられた微分方程式の両辺をラプラス変換する。![]() 世界
世界 ![]()
![]() 世界。
世界。
&=& {\mathcal L}\left[x(t)\right](s)-{\mathcal L}\left[t\right](s)\\\\ sX(s)-x(0)&=&X(s)-\frac{1}{s^2}\\\\ (s-1)X(s)&=&1-\frac{1}{s^2}\\\\ \therefore \quad X(s)&=&\frac{s^2-1}{s^2}\cdot\frac{1}{s-1}\\\\ &=& \frac{s+1}{s^2}\\\\ &=& \frac{s}{s^2}+\frac{1}{s^2}\\\\ &=& \frac{1}{s}+\frac{1}{s^2} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-64efdcfe08e8693a5f47a7e2a4afe6dc_l3.png)
これをラプラス逆変換して、
![]()
解答の過程で利用したもの
導関数 f'(x) のラプラス変換 、![]() のラプラス変換、
のラプラス変換、![]() のラプラス変換
のラプラス変換
&=&s{\mathcal L}[f(t)](s)-f(0)\\\\ {\mathcal L}[t](s)&=&\frac{1}{s^2}\\\\ {\mathcal L}[1](s)&=&\frac{1}{s} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-62ed6bb6a6cad083b4ce400179cfde35_l3.png)
ラプラス逆変換のときには、![]() と
と ![]() のラプラス変換が
のラプラス変換が ![]() 、
、![]() になることを利用した。
になることを利用した。