![]() のフーリエ級数を利用して、以下の2つの無限級数を計算する。
のフーリエ級数を利用して、以下の2つの無限級数を計算する。
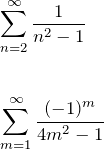
よくある問題である。
目次
1. フーリエ級数
はじめに:フーリエ級数の形
![]() と
と ![]() がそれぞれ奇関数であるため、
がそれぞれ奇関数であるため、![]() は偶関数である(下図)。
は偶関数である(下図)。
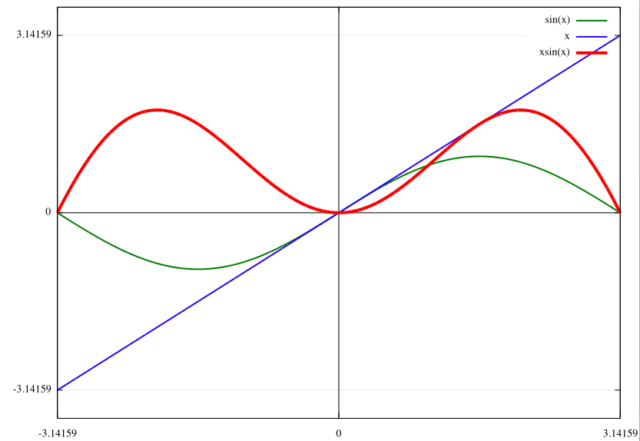
この赤線を ![]() で周期的な関数
で周期的な関数
![]()
を足し合わせて ![]() を作るのがフーリエ級数である。この問題で重要なことは、
を作るのがフーリエ級数である。この問題で重要なことは、
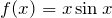 は偶関数 であるため、足し合わせる三角関数も偶関数である
は偶関数 であるため、足し合わせる三角関数も偶関数である  のシリーズを使う
のシリーズを使う
ということである。これを踏まえて ![]() をフーリエ級数で表す。
をフーリエ級数で表す。
フーリエ級数のフーリエ係数
一般に、周期 ![]() の周期関数
の周期関数 ![]() は以下のようにフーリエ級数で表すことができる。本問題の
は以下のようにフーリエ級数で表すことができる。本問題の ![]() で周期的な
で周期的な ![]() に関しては、
に関しては、
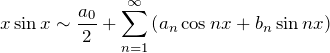
とフーリエ級数で書ける。ここで、![]() はフーリエ係数と呼ばれる。
はフーリエ係数と呼ばれる。
フーリエ係数 ![]() あるいは
あるいは ![]() を求めたい場合は、
を求めたい場合は、![]() あるいは
あるいは ![]() をかけて両辺を周期的な区間
をかけて両辺を周期的な区間 ![]() で積分してやれば良い。
で積分してやれば良い。
このとき以下の重要な積分結果を思い出す。
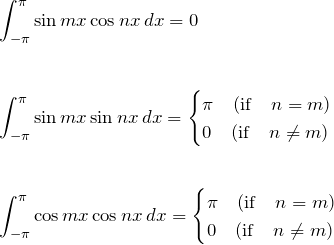
a_0 を求める
フーリエ級数の ![]() を求めるために、
を求めるために、![]() に
に ![]() をかけて
をかけて ![]() で積分しよう。青色の部分は積分するとゼロになる。
で積分しよう。青色の部分は積分するとゼロになる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{-\pi}^{\pi} x\sin x \cdot 1 \, dx &=& \int_{-\pi}^{\pi} \frac{a_0}{2} \, dx + \sum_{n=1}^{\infty} \textcolor{blue}{\int_{-\pi}^{\pi} \left(a_n \cos nx + b_n \sin x \right)\, dx}\\\\ \left[\sin x -x \cos x \right]_{-\pi}^{\pi}&=&\pi a_0\\\\\\ \therefore\quad a_0 &=&2 \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-e862de4e6af43d5f2037ca393103b53c_l3.png)
a_n を求める
次に ![]() を求める。
を求める。![]() に
に ![]() をかけて
をかけて ![]() で積分しよう。ここで、上で示した重要な積分の結果を使う、つまり、積分において
で積分しよう。ここで、上で示した重要な積分の結果を使う、つまり、積分において ![]() の
の ![]() のところ以外はすべて
のところ以外はすべて ![]() になる。
になる。
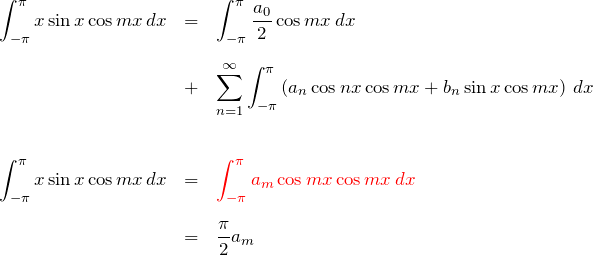
左辺の積分:
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{-\pi}^{\pi} x\sin x \cos x \, dx &=&\frac{1}{2}\int_{-\pi}^{\pi} x \sin 2x \, dx\\\\ &=& \frac{1}{2}\left[ \frac{\sin 2x}{4} - \frac{x\cos 2x}{2} \right]_{-\pi}^{\pi}\\\\ &=& -\frac{\pi}{2} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-f3e4f6e83a9d44379036c10cd3b6de81_l3.png)
より、
![]()
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{-\pi}^{\pi} x\sin x \cos mx \, dx &=& \int_{-\pi}^{\pi} x\, \frac{\sin(1+m)x+\sin(1-m)x}{2} \, dx\\\\\\ &=&\frac{1}{2}\left[ \frac{\sin(1+m)x}{(1+m)^2}-\frac{x\cos(1+m)x}{1+m} \right]_{-\pi}^{\pi}\\\\ &+&\frac{1}{2}\left[ \frac{\sin(1-m)x}{(1-m)^2}-\frac{x\cos(1-m)x}{1-m} \right]_{-\pi}^{\pi}\\\\\\ &=& \frac{1}{2(1+m)}\left[-\pi\cos(1+m)\pi -\pi\cos(1+m)(-\pi) \right]\\\\ &+& \frac{1}{2(1-m)}\left[-\pi\cos(1-m)\pi -\pi\cos(1-m)(-\pi) \right]\\\\\\ &=& \frac{-\pi}{(1+m)}\cos(m+1)\pi+ \frac{-\pi}{(1-m)}\cos(m-1)\pi\\\\ &=& \begin{cases} \frac{-\pi}{(1+m)}(-1)+ \frac{-\pi}{(1-m)}(-1) \quad({\rm if} \quad m= 2k \quad({\rm even}))\\\\ \frac{-\pi}{(1+m)}(+1)+ \frac{-\pi}{(1-m)}(+1) \quad({\rm if} \quad m= 2k+1 \quad({\rm odd})) \end{cases}\\\\\\ &=& \frac{(-1)^{m+1}}{m^2-1} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-0b17fb1b3c6ca20e73725c1c43762e7f_l3.png)
以上より、![]() がわかる。
がわかる。
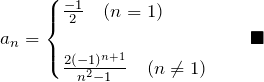
「この問題あるある」は下の通り。とくに①はフーリエ級数問題あるあるである。![]() の
の ![]() を偶奇で場合分けする。偶奇で値が
を偶奇で場合分けする。偶奇で値が ![]() か
か ![]() なので、
なので、![]() や
や ![]() で表すことができる。
で表すことができる。
b_n を求める
![]() を求めるためには、
を求めるためには、![]() に
に ![]() をかけて
をかけて ![]() で積分すればわかる。しかし、
で積分すればわかる。しかし、![]() が偶関数であることを思い出すと、
が偶関数であることを思い出すと、![]() である。つまり、
である。つまり、![]() が偶関数なので奇関数の
が偶関数なので奇関数の ![]() は使わない。
は使わない。
![]()
フーリエ級数を利用した無限級数の値①
上で求めたフーリエ係数 ![]() を代入する。
を代入する。
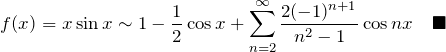
この式と求めたい下の式を比べる。
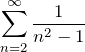
![]() であるから、
であるから、![]() とすれば良さそうである。
とすれば良さそうである。
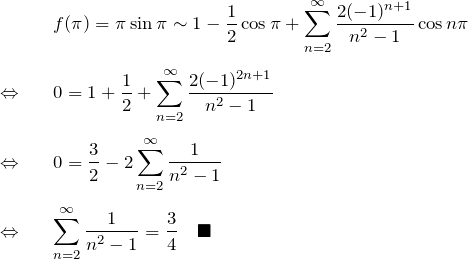
となる。この値は以下のように部分分数分解によって確認できる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\sum_{n=2}^\infty \frac{1}{n^2-1}\\\\ &&= \sum_{n=2}^\infty \frac{1}{2}\,\left[\frac{1}{n-1}-\frac{1}{n+1}\right]\\\\ &&= \frac{1}{2}\,\left[ \left(\frac{1}{1}-\cancel{\frac{1}{3}}\right)+ \left(\frac{1}{2}-\cancel{\frac{1}{4}}\right)+ \left(\cancel{\frac{1}{3}}-\cancel{\frac{1}{5}}\right)+ \dots \right]\\\\ &&=\frac{3}{4} \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-b0066799fff015af84750a1fa1f63043_l3.png)
フーリエ級数を利用した無限級数の値②
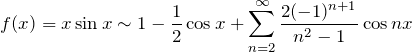
と下の式を見比べる。
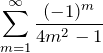
![]() と置く。このとき
と置く。このとき ![]() の値は、以下のように
の値は、以下のように ![]() が
が ![]() の倍数とそのあまりによって場合分けできる。
の倍数とそのあまりによって場合分けできる。
![]() が2以上であることに注意して、
が2以上であることに注意して、![]() が
が ![]() でない2つの場合を残して書くと、
でない2つの場合を残して書くと、
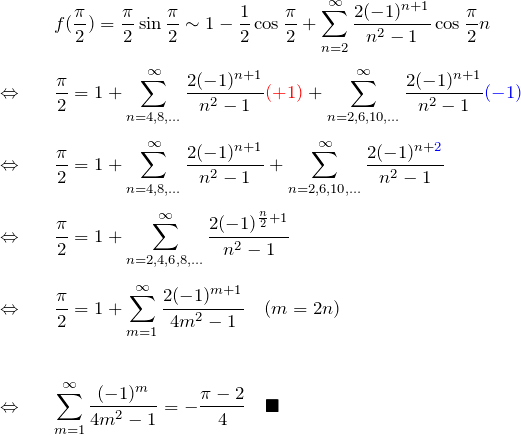
おまけ:適当に有限和にして計算した結果と右辺の差は以下のようになる。
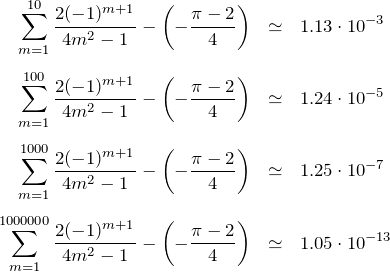
3. まとめ
具体的に ![]() のフーリエ級数を求めた。よくある問題として、フーリエ級数で展開した
のフーリエ級数を求めた。よくある問題として、フーリエ級数で展開した ![]() を用いて無限級数和を求めた。
を用いて無限級数和を求めた。
フーリエ級数を求めるときに公式は用いなかった。これは、フーリエ係数が三角関数の直交性によって簡単に計算できるということを知ってもらいたかったからである。いや、本当は、公式を覚えていない私の怠慢である。