【結合】絵で見るイオン結合(NaClの例)

　結晶における原子の結合の種類はさまざまである。ここではイオン結晶をみていきたい。陽イオンと陰イオンの静電的な結合の話であるために理解しやすいと思う。結合の種類は以下の５種類である。

• イオン結合 ←
• 共有結合
• 金属結合
• 分子間結合
• 水素結合

1. イオン結晶の概要

1.1 イオン結合の起源

　イオン結晶の代表例である塩化ナトリウム（NaCl）を見ていく。下のように電子を配置するのは正確ではないが、電子の受け渡しがわかりやすいので下の模型を使う。

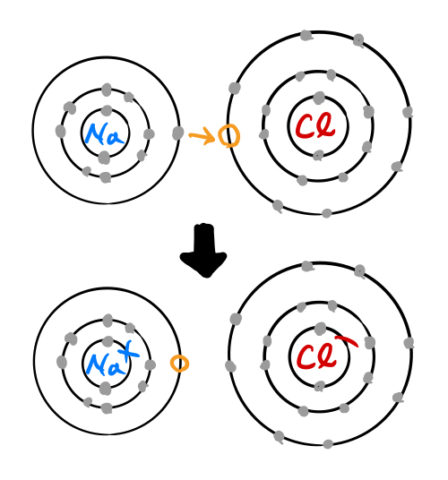
　Na：原子番号11のアルカリ金属、Cl：原子番号17のハロゲン元素である。Naは電子が１個余っているし、Clは電子１個不足しているため、Naは最外殻電子１個をClに渡す。これは互いに閉殻を作って安定化しようとするためである。

　GaAsなどのⅢ-Ⅴ族半導体と異なり、余っている電子はほとんどClのものになる（図の矢印の下）。したがって、Cl原子は電子１個を得てClイオンとなる（陰イオン）。一方で、Na原子は電子１個を与えてNaイオンとなる（陽イオン）。

　イオン結晶は電子の所在がかなりはっきりしている。したがって、２種類の原子は陽イオンと陰イオンにはっきり分かれている。

　違う電荷をもった粒子は互いに引き付け合う引力が働くし、同じ電荷を持った粒子は互いに退け合う斥力が働く。陽イオンと陰イオンも同様に引力的な力が働く。このような正負の静電的な力がイオン結合の起源となる。

1.2 イオン結晶をみる

　先ほどの模型をもう少し発展させて、電子が雲のように広がっているとしてNaイオンとClイオンを描いてみた。

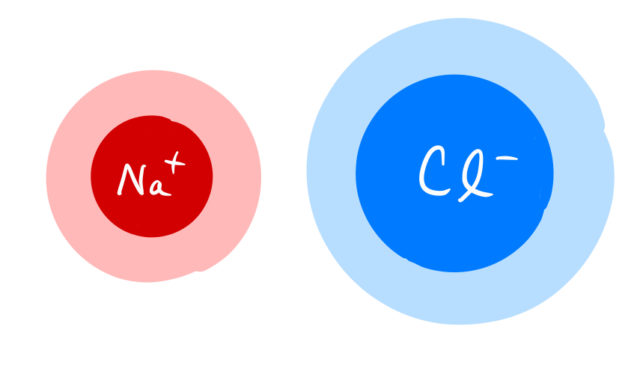
　プラスとマイナスが引きつけ合うという静電的な力（イオン結合）により、NaイオンとClイオンは互いに交互に配列する塩化ナトリウム型(NaCl型； 岩塩型)構造をとる。

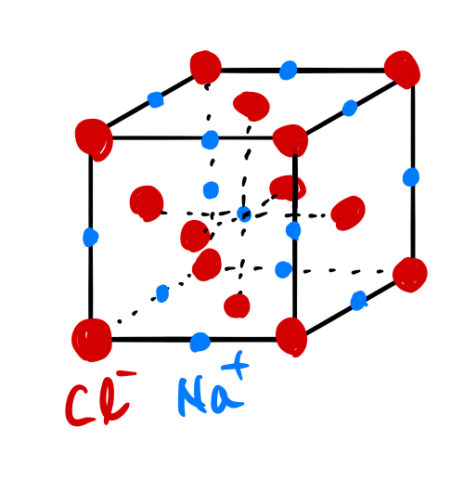
　NaCl型構造をとるイオン結晶は他に、MgOやCaOなどがある。イオン結晶はこのNaCl型構造以外に、塩化セシウム(CsCl)型、閃亜鉛鉱(ZnS)型、ホタル(CaF)石型、ルチル(TiO)型などがある。

1.3 ポテンシャルエネルギーをみる

　プラスとマイナスが引き合うなら、いっそのこと陽イオンと陰イオンくっつければいいじゃないか、と考えるかもしれない。しかし、実際にはイオン同士は適度な距離（平衡位置）を保って結晶を作る。

　すなわち、イオン同士を離れさせる何かしらの「斥力」が働いているのである。

　この斥力の起源は、電子が同一の状態をとることができないとする「パウリの排他原理」である。電子の波動関数を用いた説明になるため、この量子力学的な効果についてはここでは立ち入らない。とにかく、イオンが近づきすぎるとエネルギーの高い状態を取らないといけなくなる、ということが斥力の原因である。

　下の図は原子間距離を横軸にとり、縦軸にポテンシャルエネルギーをとったものである。オレンジ色がクーロン力による静電エネルギー、緑色が斥力エネルギーである。黒い太線は全エネルギーで（静電エネルギー）＋（斥力エネルギー）を表す。

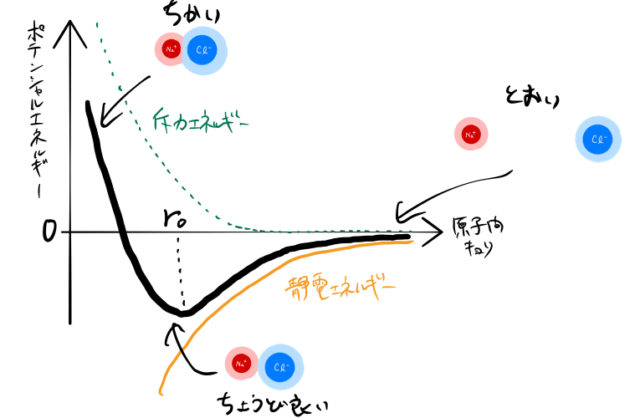
　この図から、以下のことがわかる。

• 原子間距離が大きいと、静電エネルギーも斥力エネルギーも小さく全エネルギーは０に近い。
• 原子間距離が小さいと、斥力エネルギーが静電エネルギーに打ち勝ち、全エネルギーは大きくなる。
• ある平衡位置 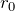のところで全エネルギーは最小値をとり、安定化する。

結局、斥力エネルギーと静電エネルギーがバランスがとれた位置で安定化し、平衡状態になる。

2. 原子をバラバラにする

2.1 凝集エネルギー（結合エネルギー）

　凝集エネルギーは、原子が集まってできた結晶をばらばらの原子（分子）にするのに必要なエネルギーである。

　上で見てきたように、イオン結晶の場合はイオン結合で結合している。原子をばらばらにするためには、平衡位置にある陽イオンと陰イオンを無限遠まで持って行けば良い。

　先ほどのポテンシャルエネルギーの図で言えば、平衡位置 から原子間距離を無限にすればよい。そのときに必要なエネルギーは最小値である窪みの位置から、無限に右に行ったほぼ平坦な位置（エネルギー0）までの差である。

　したがって、イオン１対あたりの結合エネルギーは、 におけるエネルギーと同じである。

2.2 マーデルング定数とは

　マーデルング定数（Madelung constant）は結合エネルギーを考える上で重要である。NaCl型構造について見てみる。

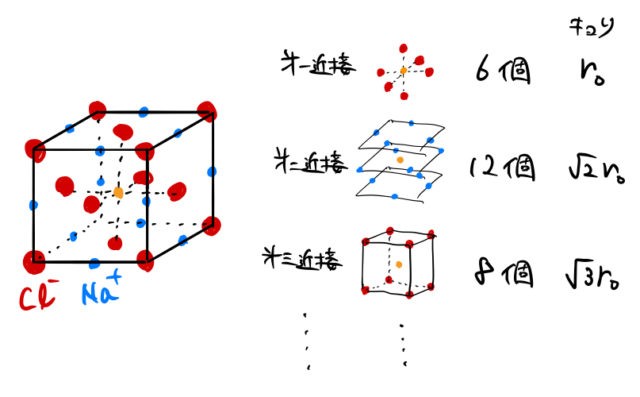
　真ん中のオレンジの原子（Na）は他のすべてのイオンから静電的なクーロン力を受けている。

　ここで２つの点電荷が距離 にあるときに、点電荷をクーロン力を振り切って無限遠までもっていくときに必要なエネルギーは、

   

で表されて、距離 に反比例することを思い出そう。

　今考えてる結晶内のオレンジの原子を無限遠に持っていくためには、すべてのクーロン力を振り切る必要がある。規則的に並んだ結晶の場合は、第一近接原子（最近接原子）、第二近接原子、第三近接原子、…と原子の個数と原子間距離を足し合わせれば良い。

　したがって、オレンジの原子を無限遠に持っていくのに必要なエネルギーは、

   

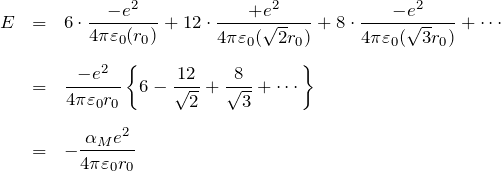
である。最後の行で、カッコのところがマーデルング定数 に対応する部分である。このマーデルング定数 は結晶構造のみによって決まっている値である。NaCl型構造の場合は、 である。

2.3 なぜマーデルングエネルギーは過大評価する？

　 で表した上の式のマーデルングエネルギーで結合エネルギーを計算すると実験値より大きく見積もることが知られている。なぜだろうか。

　2.1 の話を思い出してほしい。マーデルングエネルギーは静電エネルギーしか考慮されていないのである。したがって、実際に存在する斥力エネルギーの分だけ、原子はバラバラにしやすいだろう。

　実際にイオン結晶の結合エネルギーを計算で求めたいときには、

• マーデルングエネルギーを計算する
• 斥力エネルギーを計算する

ことができれば良い。

　簡単に斥力エネルギーを求めれば良い、と書いたがこれは意外に難しい。というのも斥力エネルギーの起源は量子力学的な効果に由来していたからである。このような理由から、実際に斥力エネルギーを計算したい場合は、弾性定数などを用いて間接的に大きさが見積もられる。

3. まとめ

　イオン結晶を見てきた。量子力学の内容になるべく触れないで結合の様子を説明した。イオン結晶には、陽イオンと陰イオンの静電的な結合以外に、電子間の斥力があることは覚えておきたい。