1次元の自由振動は単振動と呼ばれ、高校物理でも一応は扱う。ここで学ぶ自由振動は下に挙げた減衰振動、強制振動などの基礎になる。上の4つの振動は変位 ![]() が微小のときの話である。
が微小のときの話である。
- 自由振動(単振動):
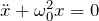
- 減衰振動:
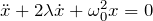
- 強制振動(摩擦無し):
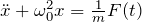
- 強制振動(摩擦あり):
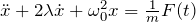
- 非調和振動:(非線形の微分方程式)
一般解は下の形になる。
![]()
1. 自由振動の運動方程式
1.1 自由振動のラグランジアン
ラグランジアン ![]() をつくる。変位
をつくる。変位 ![]() が小さい時は
が小さい時は
- 運動エネルギー:
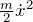
- ポテンシャルエネルギー:
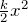
である。
したがって、![]() (運動エネルギー)–(ポテンシャルエネルギー)より
(運動エネルギー)–(ポテンシャルエネルギー)より
![]()
1.2 ラグランジュ方程式 → 運動方程式
ラグランジュ方程式:
![]()
に上の ![]() を代入するとニュートンの運動方程式が求められる。
を代入するとニュートンの運動方程式が求められる。
運動方程式:
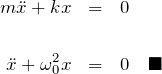
ここで、![]() と置いた。
と置いた。
1.3 運動方程式の解
運動方程式は線形微分方程式である。
よく知られているように一般解は2つの独立な解から成る:
![]()
![]() と
と ![]() の関係:
の関係:
![]()
より、
![]()
である。
各項の説明:
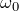 :角振動数
:角振動数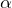 :初期位相
:初期位相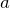 :自由振動の振幅
:自由振動の振幅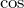 の引数(中身):位相
の引数(中身):位相
1.4 複素振幅で表す
三角関数を複素数で表すと微分積分などが便利である。上の三角関数の一般解を複素数で表す。
![Rendered by QuickLaTeX.com \begin{eqnarray*} x&=&a\cos{(\omega_0 t+ \alpha)}\\ \\ &=&{\rm Re}\left[ ae^{-i(\omega_0 t+ \alpha)}\right] \\ \\ &=& {\rm Re}\left[ ae^{-i\alpha}e^{-i\omega_0 t}\right] \\ \\ &=& {\rm Re}\left[Ae^{-i\omega_0 t}\right] \quad(A=ae^{-i\alpha}) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-9f53c5a4f0a4f854aa007b6928e3d2ff_l3.png)
応用上は、複素数のまま計算して最後に実部 Re をとる。
1.5 自由振動のエネルギー
系のエネルギーは、![]() (運動エネルギー)
(運動エネルギー)![]() (ポテンシャルエネルギー)より、
(ポテンシャルエネルギー)より、
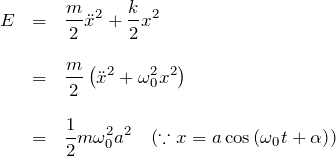
この形から分かるように自由振動のエネルギーは振幅 ![]() の2乗に比例する。ただし、振幅に対応する変位
の2乗に比例する。ただし、振幅に対応する変位 ![]() が小さいときの話である。
が小さいときの話である。
2. まとめ
自由振動は変位が小さい時の振動(微小振動)であることは覚えておきたい。同じ微小振動として、減衰振動、強制振動の基礎にもなる。一般解、エネルギーなどは高校物理でもよく見かけるので理工学系の大学生以上なら問題はないと信じたい。