逆格子ベクトルの定義より以下の関係が簡単にわかります。
体積の関係式
![]()
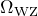 :ウィグナーザイツセルの体積(実空間)
:ウィグナーザイツセルの体積(実空間)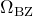 :第一ブリルアンゾーンの体積(逆空間)
:第一ブリルアンゾーンの体積(逆空間)
1. 逆格子ベクトルの定義と基本事項まとめ
定義だけ載せておきます。

簡単なまとめ:
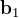 は
は 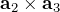 方向にあるため、
方向にあるため、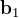 と
と 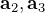 は直交。
は直交。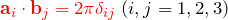
実空間の体積に関するまとめ:
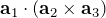 (スカラー三重積)は平行六面体(単位胞)の体積を表す。
(スカラー三重積)は平行六面体(単位胞)の体積を表す。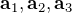 で作られる平行六面体の中に(実)格子点は1個
で作られる平行六面体の中に(実)格子点は1個- ウィグナーザイツ(WZ)セル内に含まれる(実)格子点は1個
これらから
ポイント
![]() =(平行六面体の体積)=(WZセルの体積
=(平行六面体の体積)=(WZセルの体積 ![]() )
)
がわかる。なぜなら格子点1個が占める体積は同じであるため。
逆空間の体積の関係も同じである。
ポイント
![]() =(平行六面体の体積)=(1stBZの体積
=(平行六面体の体積)=(1stBZの体積 ![]() )
)
あとは ![]() と
と ![]() の関係を調べる。
の関係を調べる。
2. 定義に基づいたベクトル計算
![]() を計算する。
を計算する。
![]() について:
について:
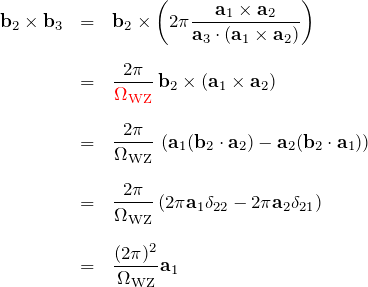
- 2つ目の等号:
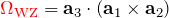
- 3つ目の等号:BAC-CAB則(
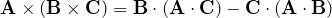 )
) - 4つ目の等号:
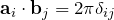
よって、
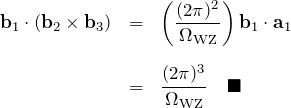
3. 計算しなくても?
![]() が現れるイメージを説明しよう。逆格子ベクトルの定義より、
が現れるイメージを説明しよう。逆格子ベクトルの定義より、
![]()
である。これは逆格子点の点間隔は、実格子点の点間隔の逆数に 2![]() をかければ良いことがわかる。立方晶系を例にとれば、実空間の立方体の1辺を大きくする(体積が大きい)と逆空間の立方体の1辺は小さくなる(体積が小さい)。
をかければ良いことがわかる。立方晶系を例にとれば、実空間の立方体の1辺を大きくする(体積が大きい)と逆空間の立方体の1辺は小さくなる(体積が小さい)。
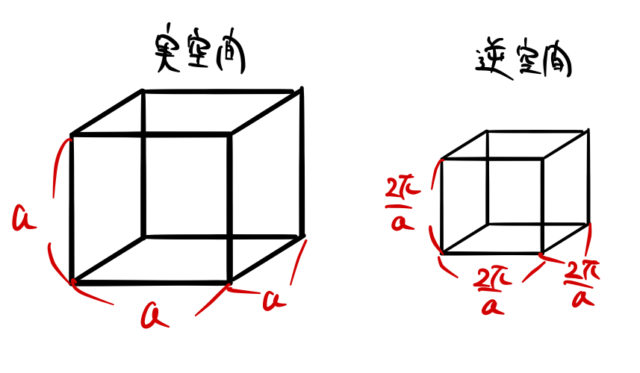
結局、WZと1stBZの体積の関係はより一般的な以下の関係を満たす。
体積の関係式
![]()
 :逆格子点1個を含む単位胞の体積
:逆格子点1個を含む単位胞の体積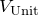 :実格子点1個を含む単位胞の体積
:実格子点1個を含む単位胞の体積
単位胞(単位格子)は、敷き詰めて空間全体を埋めれる空間格子の取り方で、任意の形にとっても良い。
4. まとめ
逆格子ベクトルの定義からウィグナーザイツセルの体積と第一ブリルアンゾーンの体積の関係を示した。また、これはより一般的な格子点1個を含む単位胞の体積の関係に他ならないということがわかる。結局、「格子点1個が占める空間の体積」が重要である。
逆格子ベクトルは固体物性で重要なのでしっかり押さえておきたい。