例題
![]() で周期的な以下の関数
で周期的な以下の関数 ![]() をフーリエ級数に展開せよ。
をフーリエ級数に展開せよ。
![]()
1. 準備
グラフの概形
![]() のグラフは下のようになる。
のグラフは下のようになる。
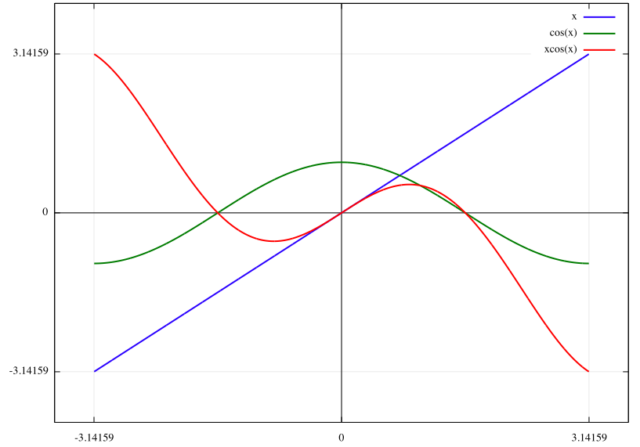
この関数は ![]() で奇関数である。
で奇関数である。
フーリエ級数展開/フーリエ係数
フーリエ級数で基本的に使うのは三角関数の直交性である。
三角関数の直交性
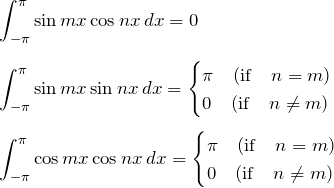
2.【解答】
周期関数 ![]() をフーリエ級数展開する。すなわち、周期
をフーリエ級数展開する。すなわち、周期 ![]() の三角関数で展開する。
の三角関数で展開する。
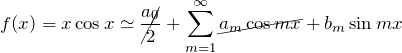
![]() は奇関数であるため、奇関数の
は奇関数であるため、奇関数の ![]() のみで展開できる。
のみで展開できる。![]() の両辺に
の両辺に ![]() をかけて、
をかけて、![]() で積分する。
で積分する。
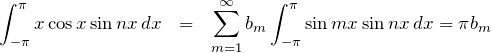
よって、
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} b_n&=&\frac{1}{\pi}\int_{-\pi}^{\pi} x\cos x \sin nx\, dx\\\\ &=& \frac{1}{2\pi}\int_{-\pi}^{\pi}x\left\{ \sin(n+1)x+\sin(n-1)x\rihgt\}\,dx\\\\ &=& \frac{1}{2\pi}\left\{ \left[\frac{sin(n+1)x}{(n+1)^2}-\frac{x\cos(n+1)x}{n+1} +\frac{sin(n-1)x}{(n-1)^2}-\frac{x\cos(n-1)x}{n-1} \right]_{-\pi}^{\pi} \right\}\\\\ &=& frac{1}{2\pi}\left\{ -\frac{2\pi}{n+1}\cos(n+1)\pi-\frac{2\pi}{n-1}\cos(n-1)\pi \right\}\\\\ &=& -\frac{(-1)^{n+1}}{n+1}-\frac{(-1)^{n-1}}{n-1}\\\\ &=& \frac{2n(-1)^n}{n^2 - 1}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-e4f79e389850c3050668bf357f6582e3_l3.png)
![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} b_1&=&\frac{1}{\pi}\int_{-\pi}^{\pi} x\cos x \sin x\, dx\\\\ &=& \frac{1}{2\pi}\int_{-\pi}^{\pi}x\sin 2x \,dx\\\\ &=& \frac{1}{2\pi}\left[ \frac{\sin 2x}{4}-\frac{x\cos 2x}{2} \right]_{-\pi}^{\pi}\\\\ &=& \frac{1}{2\pi}\left[ -\frac{\pi}{2}\cos2\pi -\frac{\pi}{2}\cos(-2\pi)\right]\\\\ &=& -\frac{1}{2}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-e9ddf609deb2fe178da54b39eb45e2a5_l3.png)
以上より、![]() のフーリエ級数展開は、
のフーリエ級数展開は、
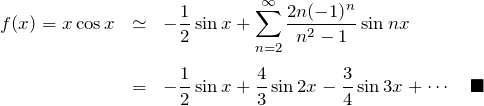
下図は、(左)第3項までのフーリエ級数展開、(右)第6項までのフーリエ級数展開である。
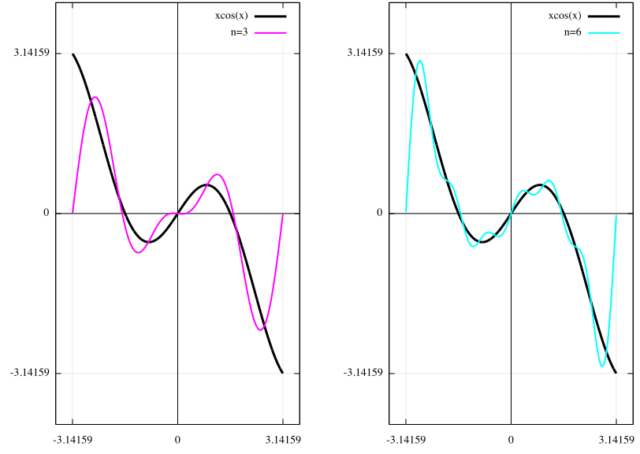
3. まとめ
奇関数なので、フーリエ係数を求める計算は苦労しないだろう。