関数を余弦(cos)と正弦(sin)に展開する問題である。
例題
![]() で周期的な以下の関数
で周期的な以下の関数 ![]() をフーリエ余弦級数とフーリエ正弦級数に展開せよ。
をフーリエ余弦級数とフーリエ正弦級数に展開せよ。
![]()
1. 方針
余弦級数/正弦級数
![]() のグラフは下図(a)のように周期的な
のグラフは下図(a)のように周期的な ![]() のグラフになる。
のグラフになる。
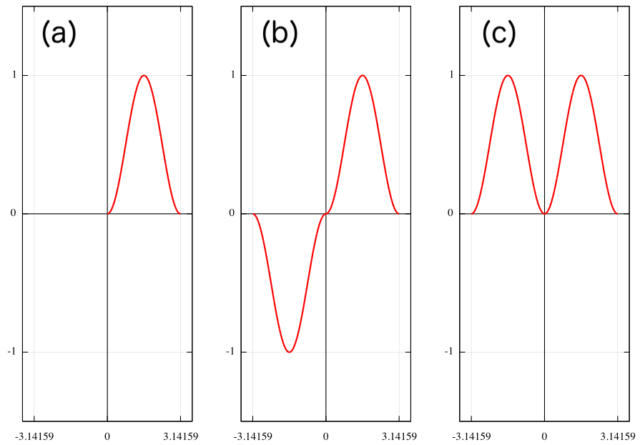
フーリエ正弦級数・余弦級数の問題は以下のように考える。
- 正弦級数:図(b) のように奇関数になるように折り返し
- 余弦級数:図(c) のように偶関数になるように折り返し
を考えれば良い。
フーリエ級数展開/フーリエ係数
フーリエ級数で基本的に使うのは三角関数の直交性である。
三角関数の直交性
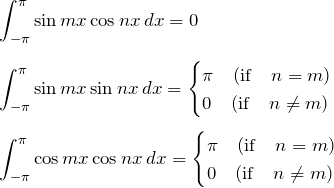
2. 解答
1. フーリエ余弦級数に展開
区間を ![]() から
から ![]() にしてやる。
にしてやる。
![]()
ここで、
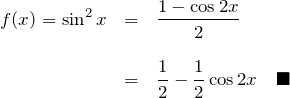
となる。具体的なフーリエ係数は
![]()
※この例題の ![]() のように特殊な場合は、フーリエ係数を求めるための積分計算は不要である。もちろん、積分計算をしても同様の結果を得る。
のように特殊な場合は、フーリエ係数を求めるための積分計算は不要である。もちろん、積分計算をしても同様の結果を得る。
2. フーリエ正弦級数に展開
上の図(b) のように、奇関数になるように折り返すと、
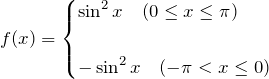
である。これをフーリエ級数展開すればよい。
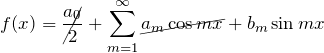
![]() が奇関数であるため、奇関数の
が奇関数であるため、奇関数の ![]() のみで展開できる(正弦級数)。両辺に
のみで展開できる(正弦級数)。両辺に ![]() をかけて、
をかけて、![]() で積分する。
で積分する。
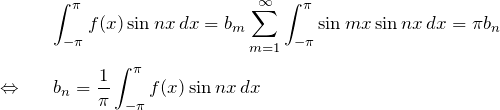
![]() は偶関数である。したがって、
は偶関数である。したがって、
![Rendered by QuickLaTeX.com \begin{eqnarray*} b_n&=& \frac{2}{\pi}\int_{0}^{\pi} \sin^2 x \sin nx\, dx\\\\ &=& \frac{2}{\pi}\int_{0}^{\pi} \frac{1-\cos 2x}{2}\cdot \sin nx\, dx\\\\ &=& \frac{1}{\pi}\int_{0}^{\pi} \sin nx\, dx -\frac{1}{\pi}\int_{0}^{\pi} \cos 2x\, \sin nx\, dx\\\\ &=& \frac{1}{\pi}\left[-\frac{1}{n}\,\cos nx\right]_{0}^{\pi}\\ &&\quad - \frac{1}{\pi}\int_{0}^{\pi} \frac{1}{2}\left(\sin (n+2)x +\sin(n-2)x \right) \, dx\\\\ &=& \frac{1}{n\pi}\left[1-(-1)^n\right]\\ &&\quad - \frac{1}{2\pi}\left[-\frac{1}{n+2}\cos(n+2)x -\frac{1}{n-2}\cos(n-2)x\right]_{0}^{\pi}\quad(n\neq 2)\\\\ &=& \frac{1}{n\pi}\left[1-(-1)^n\right]\\ &&\quad -\frac{1}{2\pi(n+2)}\left[1-(-1)^n\right] -\frac{1}{2\pi(n-2)}\left[1-(-1)^n\right]\\\\ &=& \frac{1}{2\pi}\left(\frac{2}{n}-\frac{2}{n+2}-\frac{2}{n-2}\right)\left(1-(-1)^n\right)\\\\ &=& \frac{-4}{n(n-2)(n+2)}\,\left(1-(-1)^n\right)\\\\ &=& \begin{cases} \frac{-8}{n(n-2)(n+2)}\quad(n:\;{\rm odd})\\\\ 0\quad(n:\;{\rm even},n\neq 2) \end{cases} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-de9ee3a056a23451a5c4dbab0abbf974_l3.png)
また、![]() のとき:
のとき:
![Rendered by QuickLaTeX.com \begin{eqnarray*} b_2&=& \frac{1}{n\pi}\left[1-(-1)^n\right]-\frac{1}{\pi}\int_{0}^{\pi} \frac{1}{2}\left(\sin (n+2)x +\cancel{\sin(n-2)x} \right)\,\dx\\\\ &=& 0-\frac{1}{2\pi}\left[-\frac{1}{4}\,\cos 4x\right]_0^{\pi}\\\\ &=& 0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-fcdd79e5064018bd575083283156865c_l3.png)
以上よりフーリエ係数は、
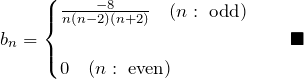
![]() のフーリエ余弦級数は、
のフーリエ余弦級数は、
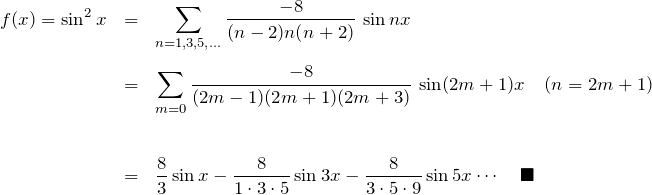
※ ![]() は連続する3つの奇数。
は連続する3つの奇数。
3. まとめ
フーリエ余弦級数・正弦級数の問題は範囲を広げて折り返せば良い。