例題
![]() で周期的な以下の関数
で周期的な以下の関数 ![]() をフーリエ級数に展開せよ。
をフーリエ級数に展開せよ。
![]()
1. 解答
![]() のグラフは下のように周期的な
のグラフは下のように周期的な ![]() のグラフになる。
のグラフになる。
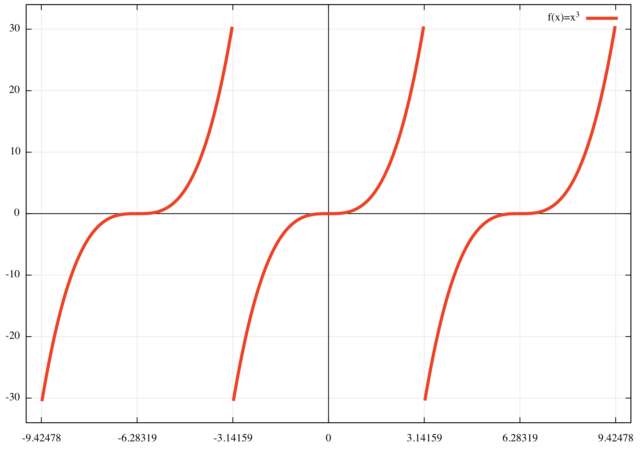
この関数は ![]() で奇関数である。
で奇関数である。
フーリエ級数展開/フーリエ係数
フーリエ級数で基本的に使うのは三角関数の直交性である。
三角関数の直交性
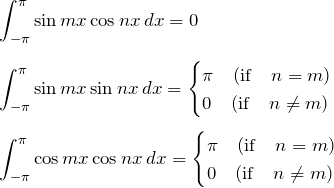
【解答】
周期関数 ![]() をフーリエ級数展開する。すなわち、周期
をフーリエ級数展開する。すなわち、周期 ![]() の三角関数で展開する。
の三角関数で展開する。
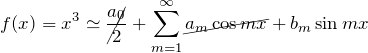
ここで、![]() が奇関数であるため、偶関数である
が奇関数であるため、偶関数である ![]() のフーリエ係数について
のフーリエ係数について ![]() である。
である。
![]() について:
について:
![]() をフーリエ級数に展開した式に
をフーリエ級数に展開した式に ![]() をかけて、
をかけて、![]() で積分する。
で積分する。
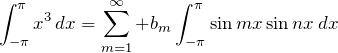
ここで、三角関数の直交性
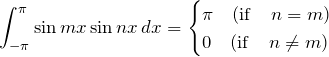
より、
![Rendered by QuickLaTeX.com \begin{eqnarray*} b_m&=&\frac{1}{\pi}\int_{-\pi}^{\pi} x^3 \, dx\\\\\\ &=& \frac{1}{\pi}\int_{-\pi}^{\pi}x^3\left(\frac{-\cos nx}{n}\right)' \, dx\\\\\\ &=& \frac{1}{\pi}\left\{ \left[-\frac{x^3 \cos nx}{n}\right]_{-\pi}^{\pi} +\frac{3}{n}\int_{-\pi}^{\pi}x^2 \cos nx \,dx \right\}\\\\\\ &=& \frac{1}{\pi}\left\{ -\frac{\pi^3 \cos n\pi}{n}+\frac{(-\pi)^3 \cos (-n\pi)}{n} +\frac{3}{n}\int_{-\pi}^{\pi}x^2 \left(\frac{\sin nx}{n}\right)' \,dx \right\}\\\\\\ &=& \frac{2\pi^2(-1)^{n+1}}{n}+\frac{3}{\pi n}\left\{ \left[x^2\frac{\sin nx}{n}\right]_{-\pi}^{\pi} -\frac{2}{n} \int_{-\pi}^{\pi}x \sin nx \,dx \right\}\\\\\\ &=&\frac{2\pi^2(-1)^{n+1}}{n} -\frac{6}{\pi n^2}\left[ \frac{\sin nx}{n^2}-\frac{x\cos nx}{n} \right]_{-\pi}^{\pi}\\\\\\ &=& \frac{2\pi^2(-1)^{n+1}}{n}-\frac{12(-1)^{n+1}}{n^3}\\\\\\ &=& \frac{2\pi^2(-1)^{n+1}}{n}\left( 1-\frac{6}{\pi^2 n^2} \right)\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-20cb66a468466b79f3176cedbed525b7_l3.png)
![]() より
より ![]() をフーリエ級数展開できる。
をフーリエ級数展開できる。
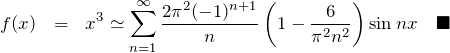
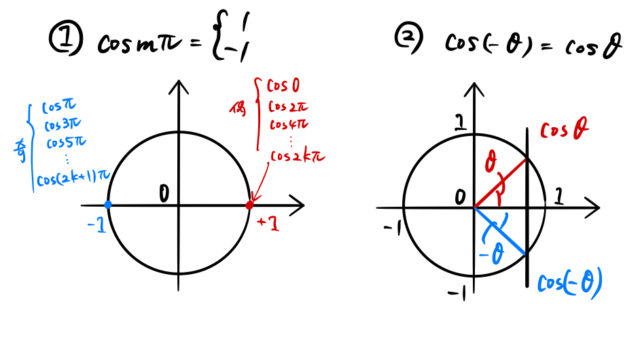
フーリエ係数計算のときによく使う下の関係をおさえておくとよい。
2. まとめ
![]() が3次関数にもなるとフーリエ係数を求める計算が大変になってくる。部分積分を丁寧に計算しておきたい。
が3次関数にもなるとフーリエ係数を求める計算が大変になってくる。部分積分を丁寧に計算しておきたい。