前回の続きから、同次型に似た例題を解いていこうと思う。 ここでは以下のタイプの微分方程式を「変数分離型」に帰着させることを目指す。
![]()
右辺の分子・分母をそれぞれ直線と見たとき、平行になる場合である。 (交点を持つ場合は、「同次型の解法の応用」で扱った。) 以下の例題を元に、上の微分方程式の解法を見ていこう。
以下の微分方程式を解け。
![]()
1. 変数分離型に帰着させるアプローチ
本問は、適当な変数変換により簡単に解くことができる。
同次型ではない
ここで扱う問題は同次型ではない。 同次型であれば、
![]()
のようにすべて係数はすべて1次式でできているはずで、 定数項は含まないのである。
平行であるという意味
2直線が平行である条件は、高校数学のレベルなので簡単にまとめておく。 2直線が平行とは「2直線の傾きが等しい」ことであった。 したがって、 以下の2直線は、ともに傾きが ![]() で平行である。
で平行である。
![]()
もし交点がある場合は、微分方程式の変数を変えてやれば解くことができた。(「同次型の解法の応用」参考)
変数変換をおこなう
結論を先に言っておくと、今回のタイプの問題は以下の変数変換により解くことができる。
![]()
と置く。すなわち、![]() に変数変換する。
平行であるがゆえ、
に変数変換する。
平行であるがゆえ、
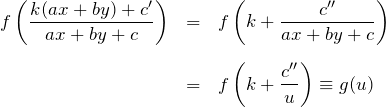
となり右辺は ![]() のみの関数でかける。
のみの関数でかける。
たとえば、
![]()
に対しては、右辺が
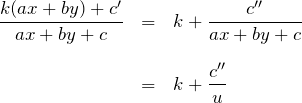
の形に書き換えることができる。
右辺は ![]() として、
として、
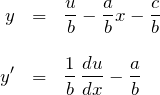
となる。
したがって、微分方程式は
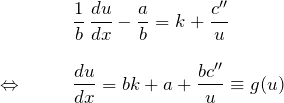
となり、![]() のみの関数
のみの関数 ![]() で表すことができ、変数分離型に帰着する。
で表すことができ、変数分離型に帰着する。
つまり、
![]()
によって
![]()
の微分方程式の解を得ることができる。
これだけだとわかりにくいため、以下の解答の流れを参考にして例題を見ていくのが良いだろう。
解答の流れ
微分方程式
![]()
に対する解答の流れを示す。
2. 例題の解答
![]()
を解く。
【解答】 式変形していく:
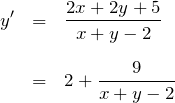
![]() と置く:
と置く:
![]()
微分方程式は
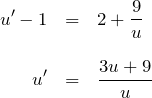
となり変数分離型に帰着する。
変数分離型を解く:
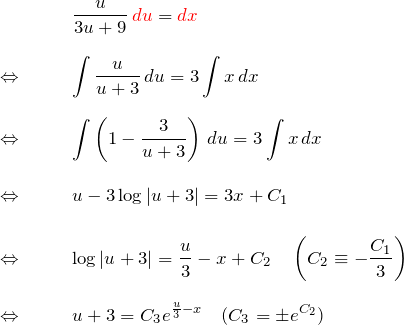
![]() に戻す:
に戻す:
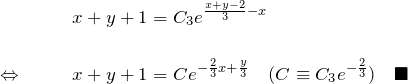
が解である。
*解のチェックのために、得られた結果を微分して元の微分方程式が得られるか調べる。最後の結果を微分する。
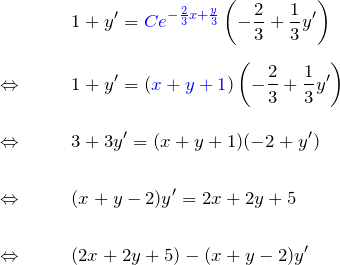
となり、元の微分方程式を得る。
3. まとめ
今回は微分方程式を簡単にしてから、適当な変数変換により変数分離型に帰着することができた。微分方程式では変数変換により、別のタイプの微分方程式に帰着することが多いため、適切な変数変換をする力を養っておくとよい。そのためにいくつかのパターンを覚えておく必要があるだろう。