ここでは孤立した多電子原子の磁性を考える。結晶中にある原子の磁性との違いを理解しておきたい。
原子の磁性を考えるときには、原子がどのような状況にあるかを考える必要がある。よくある状況は下の3つである。
- 1電子原子の磁性(孤立)
- 多電子原子の磁性(孤立)←
- 結晶中の原子の磁性(集団)
目次
1. 多電子系の角運動量
1.1 全軌道角運動量 L/全スピン角運動量 S
孤立原子における1電子の軌道角運動量 ![]() 、
、![]() とする。いま、多電子系の場合は、それぞれの電子について
とする。いま、多電子系の場合は、それぞれの電子について ![]() がある。
がある。
スピン軌道相互作用がない場合を考える。孤立した多電子系においてこれらの角運動量を総和した全軌道角運動量 ![]() 、全スピン角運動量
、全スピン角運動量 ![]() がそれぞれ一定となる。大文字の
がそれぞれ一定となる。大文字の ![]() は多電子系の角運動量、小文字の
は多電子系の角運動量、小文字の ![]() は1電子の角運動量である。
は1電子の角運動量である。
スピン軌道相互作用がない場合は、電子系のエネルギー固有値は ![]() の値によって決定される。
の値によって決定される。
1.2 全角運動量 Jとは
スピン軌道相互作用がある場合を考える。まず、それぞれの電子について
![]()
の形のスピン軌道相互作用をもつ(シュレディンガー方程式に対する相対論補正項のひとつ)。多電子系の場合は ![]() と
と ![]() を用いて、
を用いて、
![]()
の形で表すことができる。異なる電子間のスピン軌道相互作用は比較的小さいため、おおよそ ![]() に対応する。
に対応する。
スピン軌道相互作用によってスピンと軌道が混ざるため、![]() 、
、 ![]() はそれぞれ独立には保存しない。しかし、その和である全角運動量
はそれぞれ独立には保存しない。しかし、その和である全角運動量 ![]() は保存する。ここで、
は保存する。ここで、
![]()
である。
次にスピン軌道相互作用の形を変形する。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \lambda {\bf L}\cdot{\bf S} &=&\lambda\frac{1}{2}\left[ ({\bf L}+{\bf S})^2-{\bf L}^2-{\bf S}^2 \right]\\\\ &=& \frac{\lambda}{2}\left[ {\bf L}^2-{\bf L}^2-{\bf S}^2 \right]\\\\ &=& \frac{\lambda}{2} \left[J(J+1)-L(L+1)-S(S+1)\right] \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-7202d453668324b7ed4717046ba966ed_l3.png)
ここで、![]() の大きさは、
の大きさは、
![]()
のどれかである。スピン軌道相互作用の形から、
 :
:![Rendered by QuickLaTeX.com \left[J(J+1)-L(L+1)-S(S+1)\right]](https://batapara.com/wp-content/ql-cache/quicklatex.com-65aaacc828ad93a92ddd02a3ed7ebf7b_l3.png) が小さいほうがエネルギー的に得
が小さいほうがエネルギー的に得 :
:![Rendered by QuickLaTeX.com \left[J(J+1)-L(L+1)-S(S+1)\right]](https://batapara.com/wp-content/ql-cache/quicklatex.com-65aaacc828ad93a92ddd02a3ed7ebf7b_l3.png) を大きいほうがエネルギー的に得
を大きいほうがエネルギー的に得
これは後のフント則の項で使う。
1.3 ランデのg因子の導出
1電子原子の場合と同様に、ランデの ![]() 因子(Landé factor)により全角運動量
因子(Landé factor)により全角運動量 ![]() で決まった状態の磁気モーメントを考える。
で決まった状態の磁気モーメントを考える。
まず、スピン軌道相互作用がない場合の磁気モーメント ![]() は全軌道角運動量
は全軌道角運動量 ![]() と全スピン角運動量
と全スピン角運動量 ![]() に付随する磁気モーメントの和で表すことができる。
に付随する磁気モーメントの和で表すことができる。
![]()
いま、スピン軌道相互作用があるため、ある ![]() に対して上の磁気モーメントは一定ではない。実際に、
に対して上の磁気モーメントは一定ではない。実際に、![]() の状態において外磁場と相互作用する磁気モーメントは
の状態において外磁場と相互作用する磁気モーメントは ![]() の方向にある(有効磁気モーメント)。これを
の方向にある(有効磁気モーメント)。これを
![]()
とする。元の磁気モーメントとの関係は下図の通り。
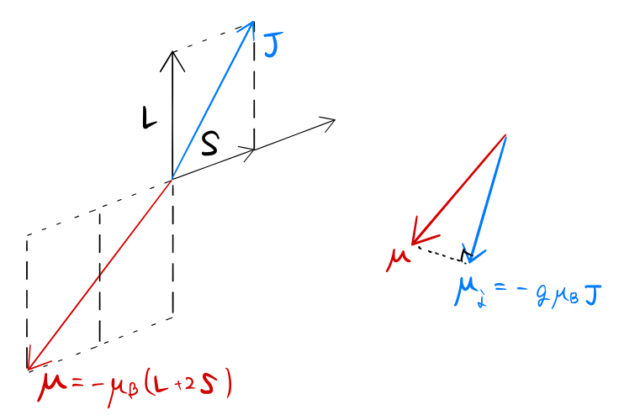
ランデの![]() 因子を求める。
因子を求める。
まず、![]() の
の ![]() 方向の成分を計算する。
方向の成分を計算する。
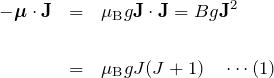
また、
![Rendered by QuickLaTeX.com \begin{eqnarray*} -{\boldsymbol \mu}\cdot {\bf J} &=&\mb \left({\bf L}+2{\bf S}\right)\cdot\left({\bf L}+{\bf S}\right)\\\\ &=&\mb \left[{\bf L}^2+2{\bf S}^2+3\textcolor{blue}{{\bf L}\cdot{\bf S}}\right]\\\\ &=&\mb \left[{\bf L}^2+2{\bf S}^2+3 \textcolor{blue}{\frac{1}{2}\left( ({\bf L}+{\bf S})^2-{\bf L}^2-{\bf S} \right)}\right]\\\\ &=&\mb \left[ \frac{3}{2}{\bf J}^2+\frac{1}{2}{\bf S}^2-\frac{1}{2}{\bf L}^2 \right]\\\\ &=&\mb \left[ \frac{3}{2}J(J+1)+\frac{1}{2}S(S+1)-\frac{1}{2}L(L+1) \right]\quad\cdots(2) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-6ee3435e2dceec594ea1f910f46ff9d3_l3.png)
(1)と(2)よりランデの ![]() 因子がわかる。
因子がわかる。
![]()
2. フント則(Hund rules)
フント則の概要を説明する。具体的な ![]() 遷移金属、
遷移金属、![]() ランタノイドの基底状態については「フント則と電子配置/ラッセル-サンダース記号」でまとめた。
ランタノイドの基底状態については「フント則と電子配置/ラッセル-サンダース記号」でまとめた。
2.1 ルール1,2とその理由
電子系の安定なエネルギー状態では以下のフント則を満たす。
以下ではフント則がどこからくるのか簡単に説明する。
ルール1の理由:![]() を最大化することにより、
交換エネルギーを最低にする。たとえば2電子の場合、交換エネルギー
を最大化することにより、
交換エネルギーを最低にする。たとえば2電子の場合、交換エネルギー ![]() は 交換積分
は 交換積分 ![]() によって表されて、スピンが平行スピンの場合にのみ正の値をとる。
によって表されて、スピンが平行スピンの場合にのみ正の値をとる。
ルール2の理由:![]() を最大化することにより、
クーロンエネルギーを最低にする。古典的な描像をとると、同じ電荷を持つ電子同士による斥力が働くため、なるべく電子同士が衝突しないような軌道をとるほうが安定する。すなわち、2つの電子が同じ向きに回っていれば衝突が少なくなるためである。
を最大化することにより、
クーロンエネルギーを最低にする。古典的な描像をとると、同じ電荷を持つ電子同士による斥力が働くため、なるべく電子同士が衝突しないような軌道をとるほうが安定する。すなわち、2つの電子が同じ向きに回っていれば衝突が少なくなるためである。
2.2 ルール3(LS結合、Jを求める)
![]() と
と ![]() の値はフント則によって決定する。そのときの
の値はフント則によって決定する。そのときの ![]() を求めてみる。フント則のルール3は以下の通りである。
を求めてみる。フント則のルール3は以下の通りである。
3. 軌道が半閉殻以下 ![]() 、半閉殻以上
、半閉殻以上 ![]()
このルールはスピン軌道相互作用のエネルギーからわかる。1.2 で述べたようにスピン軌道相互作用のエネルギーは
![]()
の形である。ここで、
 :電子のスピン軌道相互作用
:電子のスピン軌道相互作用 :正孔のスピン軌道相互作用
:正孔のスピン軌道相互作用
である。
半閉殻以下の場合(例えば14個の状態がある![]() 軌道について電子数が 7 以下の場合)、電子のスピン軌道相互作用を考える。したがって、
軌道について電子数が 7 以下の場合)、電子のスピン軌道相互作用を考える。したがって、![]() である。
である。
このとき、スピン軌道相互作用エネルギーを最小化するためには、Jを最小化すれば良い。つまり、![]() の最小値である
の最小値である ![]() とすればよい。
とすればよい。
半閉殻以上の場合(例えば14個の状態がある![]() 軌道について電子数が 7 以上の場合)、正孔のスピン軌道相互作用を考える。したがって、
軌道について電子数が 7 以上の場合)、正孔のスピン軌道相互作用を考える。したがって、![]() である。
である。
このとき、スピン軌道相互作用エネルギーを最小化するためには、Jを最大化すれば良い。つまり、![]() の最大値である
の最大値である ![]() とすればよい。
とすればよい。
以上まとめて、フント則のルール3を得る。
- 半閉殻以下 →
 →
→ 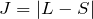
- 半閉殻以上 →
 →
→ 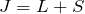
※軌道角運動量の消失がおこる ![]() 遷移金属の場合は、
遷移金属の場合は、![]() と置き換えても良い。
と置き換えても良い。
3. まとめ
多電子原子の磁性を考えた。全角運動量、ランデのg因子、フント則の概要をまとめた。フント則を用いて、![]() を決定する問題がよく出されるので例題を通して演習しておきたい。
を決定する問題がよく出されるので例題を通して演習しておきたい。