転置行列の行列式
![]()
本記事では、![]() 次正方行列
次正方行列![]() の転置行列
の転置行列 ![]() の行列式
の行列式![]() が
が ![]() と等しくなることを示す。証明する上で、行列式の定義に習熟している必要がある。
と等しくなることを示す。証明する上で、行列式の定義に習熟している必要がある。
1. 転置行列の表現
転置行列 ![]() は
は ![]() を左上から右下への対角線で折り返せば良い。3次正方行列の場合、
を左上から右下への対角線で折り返せば良い。3次正方行列の場合、
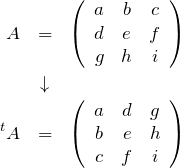
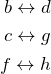
![]()
![]() 次正方行列の場合、
次正方行列の場合、
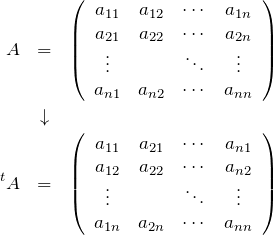
となる。
2. det(tA)=det(A) の証明
![]() 次正方行列の行列式の定義は、
次正方行列の行列式の定義は、
ここで、
![]() :置換
:置換
![]() :置換の符号
:置換の符号
![]() :置換全体の集合
:置換全体の集合
を表す。
2.1 【証明】
![]() 次正方行列
次正方行列![]() の要素を
の要素を ![]() 、
、![]() の要素を
の要素を ![]() と置く(
と置く(![]() )。
)。
行列式の定義より、
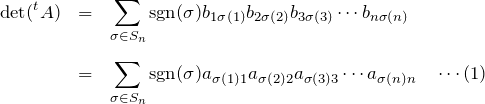
である。![]() はそれぞれが元々の
はそれぞれが元々の ![]() に一致するので、並び替えて
に一致するので、並び替えて
![]()
となる。ここで、
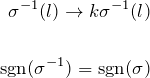
となる逆置換
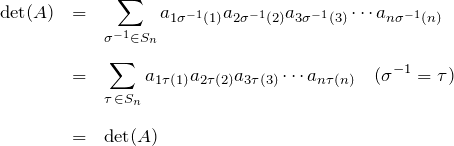
となる。
以上のように置換を使いこなし
![]()