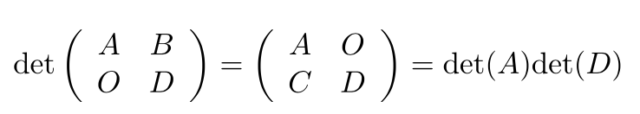行列を学ぶと「置換」という概念に出会う。どれくらい置換が有用なのかは行列式を扱っている時にわかってくる。ここでは、![]() 次正方行列の行列式を定義する。それは置換
次正方行列の行列式を定義する。それは置換 ![]() により定義されるので、置換に関する必要事項から説明する。最後には3次の正方行列の行列式に関連して、「サラスの方法」も導いている。
により定義されるので、置換に関する必要事項から説明する。最後には3次の正方行列の行列式に関連して、「サラスの方法」も導いている。
目次
1. 置換の基礎
定義を行う上で理解しておくべき知識です。
1.1 置換とは
![]() 個の文字(要素){1,2,
個の文字(要素){1,2,![]() n}から自分自身{1,2,
n}から自分自身{1,2,![]() n}への1対1の写像を考える。
n}への1対1の写像を考える。
(元の数字)![]() (行き先の数字)
(行き先の数字)
で表すとする。たとえば、{1,2,3,4}に対して、
![]()
のように置換するとする。置換を
![]()
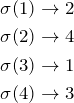
![]() 元の数字
元の数字![]() 行き先の数字
行き先の数字![]()
4つの数字のうち2個はそのままで残りの2個だけ置換する場合について考える。例えば、1と3を入れ替える場合、
![]()
![]()
何も入れ替えない置換は単位置換 ![]() を用いて、
を用いて、
![]()
![]()
1.2 巡回置換
巡回的に入れ替える場合(巡回置換)、たとえば、
![]()
![]()
1.3 置換の符号sgnと偶置換・奇置換
行列式では行の入れ替えにより符号が入れ替わる。ここでは、置換の符号sgn(![]() )を導入する。
)を導入する。
![]() が
が![]() (=偶数)回の置換を行う場合、
(=偶数)回の置換を行う場合、![]()
![]() が
が![]() (=奇数)回の置換を行う場合、
(=奇数)回の置換を行う場合、![]()
偶数回の置換を行う ![]() のものを偶置換、奇数回の置換を行う
のものを偶置換、奇数回の置換を行う ![]() のものを奇置換と呼ぶ。
のものを奇置換と呼ぶ。
1.4 置換全体の集合
2個の数字しかない {1,2} の場合、置換の方法は何通りあるだろうか。それは、単位置換と数字の入れ替え ![]() のみである。このとき、
のみである。このとき、
![]()
![]()
数字が3個ある場合の置換全体の集合
![]()
2. n次正方行列式の定義
定義:![]() 次正方行列
次正方行列 ![]() の行列式 det(
の行列式 det(![]() ) は、
) は、
![]()
などである。以下では具体的に行列式の計算をしてみる。
2.1 2次正方行列の行列式
![]() のとき、
のとき、
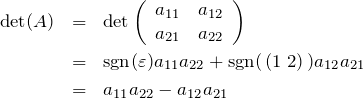
2.23次正方行列の行列式
![]() のとき、
のとき、
偶置換:![]()
奇置換:![]() であるので、
であるので、
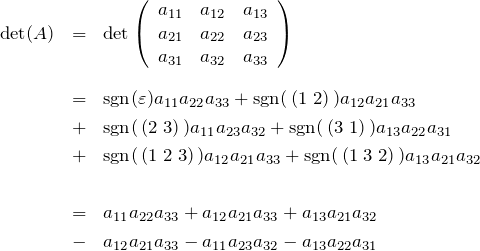
3. まとめ
置換記号 ![]() や sgn は一般化されているとわかりにくい。しかし、具体例を考えてみると非常に単純な操作をしているにすぎない、ということがわかる。行列式の定義も一見ややこしいが、2次、3次の例で十分習得できたと思う。
や sgn は一般化されているとわかりにくい。しかし、具体例を考えてみると非常に単純な操作をしているにすぎない、ということがわかる。行列式の定義も一見ややこしいが、2次、3次の例で十分習得できたと思う。
![]() と sgn を用いた行列式の定義により、様々な行列式の性質を導けるだろう。関連する記事を参照されたし。
と sgn を用いた行列式の定義により、様々な行列式の性質を導けるだろう。関連する記事を参照されたし。