H30年度の[1.1],[1.2],[3.1]のみしか解いていないです。空き時間に解きたいです。計算ミスしていたらコメントにて教えて欲しいです…
物理学[I]
1.1 平面の2質点
![]()
より、
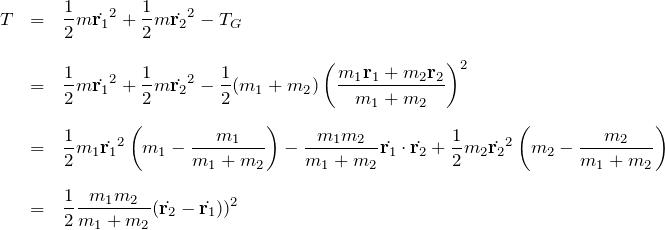
よって、換算質量 ![]() :
:
![]()
![]() と置いて、
と置いて、
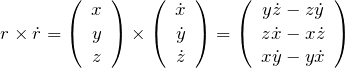
よって、
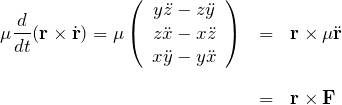
![]() は 2質点の間の引力で平面内にあるため、
は 2質点の間の引力で平面内にあるため、![]() と
と ![]() は同一平面内にあるため
は同一平面内にあるため ![]() である。
である。
![]()
となり、角運動量ベクトル ![]() は時間によらず一定である。よって、
は時間によらず一定である。よって、![]() は平面内にとどまり続ける。
は平面内にとどまり続ける。
運動エネルギー ![]() を求める。極座標表示、
を求める。極座標表示、
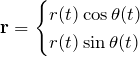
を導入する。![]() の時間微分は、
の時間微分は、
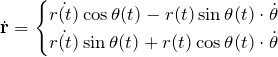
である。以降、![]() と時間依存性を省略する。運動エネルギー
と時間依存性を省略する。運動エネルギー ![]() は、
は、
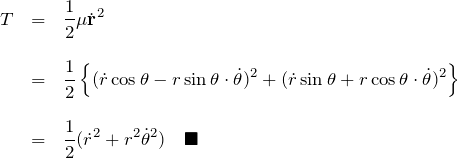
次にポテンシャルエネルギー ![]() を求める。
を求める。
2質点にはたらく引力 ![]() の大きさは
の大きさは ![]() は2質点の距離
は2質点の距離 ![]() に比例する。したがって、
に比例する。したがって、
![]()
である。よって、
![]()
となる(バネの復元力と弾性エネルギーと同じ関係)。
以上よりラグランジアン ![]() は、
は、
![]()
であり、![]() に共役な運動量
に共役な運動量 ![]() は、
は、
![]()
となる。
ここで、上記のラグランジアンを用いてオイラーラグランジュ方程式より、
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\frac{d}{dt}\textcolor{red}{\frac{\partial {\mathcal L}}{\partial \dot{\theta}}} =\frac{\partial {\mathcal L}}{\partial \theta}\\\\ &&\Leftrightarrow \frac{d\textcolor{red}{p_{\theta}}}{dt} =\frac{\partial}{\partial \theta}\left[ \frac{1}{2}(\dot{r}^2 +r^2\dot{\theta}^2)-\frac{1}{2}kr^2 \right]=0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-c32039621e8435bd03da81cc9a34bc7c_l3.png)
となり、![]() は時間によらず一定であることがわかる。
は時間によらず一定であることがわかる。![]()
[?]
1次元運動で考えたときの運動エネルギー ![]() は
は
![]()
ポテンシャルエネルギー ![]() は
は
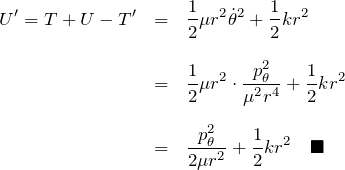
これ以降準備中。
1.2 慣性モーメント
2.1 電場・磁場
[準備中]
2.2 電磁波
[準備中]
3.1 井戸型ポテンシャル
3.2 角運動量
これの解答は簡単に。
![]() : 主量子数、
: 主量子数、![]() :方位量子数、
:方位量子数、![]() :磁気量子数
:磁気量子数 ![]()
![]()
より、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \hat{l}_+\hat{l}_-&=& (\hat{l}_x + i\hat{l}_y)(\hat{l}_x - i\hat{l}_y)\\\\ &=& \hat{l}_x^2-i\hat{l}_x\hat{l}_y+i\hat{l}_y\hat{l}_x+\hat{l}_y^2\\\\\\ \hat{l}_-\hat{l}_+&=& (\hat{l}_x - i\hat{l}_y)(\hat{l}_x + i\hat{l}_y)\\\\ &=& \hat{l}_x^2+i\hat{l}_x\hat{l}_y-i\hat{l}_y\hat{l}_x+\hat{l}_y^2\\\\\\ \therefore \hat{l}_x^2+\hat{l}_y^2&=& \frac{1}{2}\left[\hat{l}_+\hat{l}_- + \hat{l}_-\hat{l}_+ \right]\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-4c4269291699cac4e87682c5b5c0eae3_l3.png)
これより、![]() について
について
![Rendered by QuickLaTeX.com \begin{eqnarray*} \hat{l}^2&=&\hat{l}_x^2+\hat{l}_y^2+\hat{l}_z^2\\\\ &=&\frac{1}{2}\left[\hat{l}_+\hat{l}_- + \hat{l}_-\hat{l}_+ \right]+\hat{l}_z^2 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-2ac75067a167ae46282c18d8bb17e91e_l3.png)
である。これを 球面調和関数 ![]() に作用させる。
に作用させる。
![]()
第一項:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{1}{2}\hat{l}_+\hat{l}_- Y_l^m(\theta,\phi) &=& \frac{1}{2}\hat{l}_+ \left[\hbar\sqrt{(l-m)(l+m+1)}Y_l^{m+1}(\theta,\phi) } \right]\\\\ &=& \frac{\hbar}{2} \sqrt{(l-m)(l+m+1)} \hat{l}_+ Y_l^{m+1}(\theta,\phi) \\\\ &=& \frac{\hbar^2}{2}(l-m)(l+m+1)Y_l^m(\theta,\phi) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-797ff270718dfbc2d1bb57026abdb2ba_l3.png)
第二項:
![]()
第三項:
![]()
である。ここで、
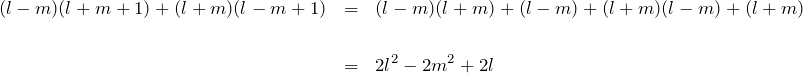
である。したがって、第一項から第三項までを足して、
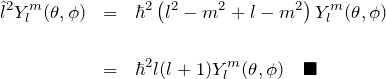
これ以降については[準備中]
4.1 分配関数
[準備中]
参考になりました!
ありがとうございます!