全記事一覧 > 物理 > 塑性力学

n乗硬化塑性体のくびれ発生条件

塑性力学では、真応力-真ひずみ曲線を簡単な近似式で表すことがある。ここでは、真応力 \sigma が真ひずみ \varepsilon の n 乗に比例する「n乗硬化塑性体」のくびれ発生条件を見よう。
n乗硬化塑性体のくびれ発生条件

\varepsilon = n

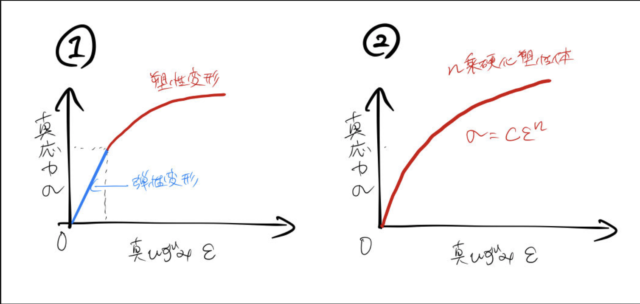
1. 真応力-真ひずみ曲線

　まず、一般的な真応力-真ひずみ曲線は①に示す。材料を引っ張ると、まず真ひずみの小さい領域で弾性変形がおこる。弾性変形はいわゆるバネと同じで、材料を引っ張るのをやめると元の状態に戻る。真ひずみの大きい領域は塑性変形であり、この領域で変形した材料は元の状態には戻らない。

2. n乗硬化塑性体

　①の一般的な曲線を n乗硬化塑性体 として近似したものを②に示す。後に示すように簡単な式ではあるが、①の曲線をうまく表現できるのでよく用いられる。

2.1 くびれ発生条件の計算

　真応力は塑性係数 c を用いて、

    \begin{eqnarray*}\sigma = c \varepsilon^n\end{eqnarray*}

 
で与えられる。n は加工硬化指数で、0から1の間の値をとる。くびれ発生条件は、

    \begin{eqnarray*}\frac{d\sigma}{d\varepsilon}=\sigma\end{eqnarray*}

 
である。 したがって、n乗硬化塑性体のくびれ発生条件は、

    \begin{eqnarray*}\frac{d(c\varepsilon^n)}{d\varepsilon}&=&c\varepsilon^n\\ \\\leftrightarrow cn\varepsilon^{n-1}&=& c\varepsilon^n\\ \\\leftrightarrow c\varepsilon^{n-1}(\epsilon-n)&=&0\\ \\\therefore \; \varepsilon &=& n\end{eqnarray*}

 
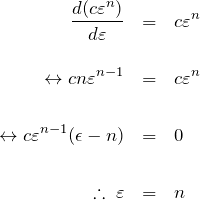
である。真ひずみ \varepsilon が加工硬化指数 n の値に到達した時にくびれが発生する。


コメントを残す

メールアドレスが公開されることはありません。