例題
また、この結果を用いて、
![]() で周期的な以下の関数
で周期的な以下の関数 ![]() をフーリエ級数に展開せよ。
をフーリエ級数に展開せよ。
![]()
また、この結果を用いて、
![]()
この関数はジグザグである。かなり![]() に形が似ている。たとえば、
に形が似ている。たとえば、![]() と
と ![]() を比較してみると下のようになる。
を比較してみると下のようになる。
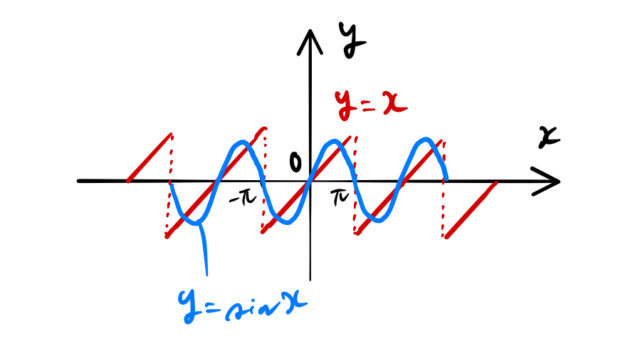
フーリエ級数で基本的に使うのは三角関数の直交性である。
三角関数の直交性
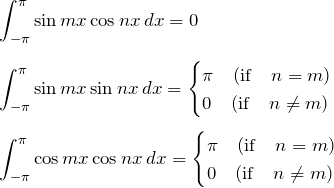
【解答】
![]() をフーリエ級数で展開する。
をフーリエ級数で展開する。
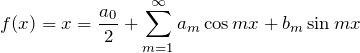
奇関数のフーリエ級数展開:
ここで、![]() は奇関数である。したがって、奇関数である
は奇関数である。したがって、奇関数である ![]() のシリーズで展開でき、偶関数の
のシリーズで展開でき、偶関数の ![]() のシリーズについては
のシリーズについては ![]() となる。
となる。
![]() を求める:
を求める:
両辺に ![]() をかけて、
をかけて、![]() で積分すると、
で積分すると、

三角関数の直交性から ![]() となる
となる ![]() 同士以外はすべて0になる。また、
同士以外はすべて0になる。また、![]() の
の![]() の積分の値は
の積分の値は ![]() になる。したがって、
になる。したがって、
![]()
より、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \textcolor{red}{a_n}&=&\frac{1}{\pi}\int_{-\pi}^{\pi} x \sin nx\,dx\\\\ &=&\frac{1}{\pi} \left[\frac{\sin nx}{n^2}-\frac{x\cos nx}{n}\right]{-\pi}^{\pi}\\\\ &=& \frac{1}{\pi}\left\{ \left(-\frac{1}{n}\right) \pi \cos m\pi -(-\pi)\cos \left(-m\pi\right) \right\} \\\\ &=& \frac{-2}{n}\,\textcolor{red}{\cos\pi}\\\\ &=& \frac{2\,(-1)^{n+1}}{n}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-1d8019e5cc88da612e0c18f3896295af_l3.png)
※フーリエ係数の計算でよく使うのは下の関係である。
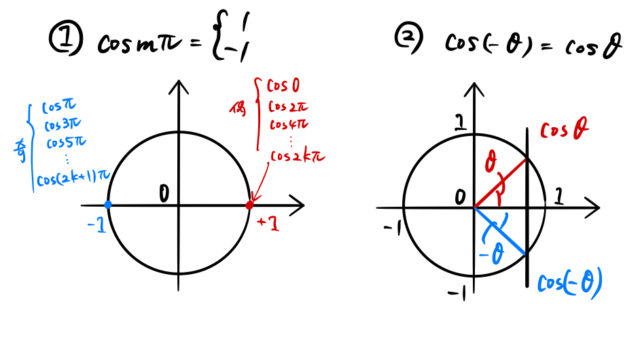
以上より、![]() をフーリエ級数で表すと、
をフーリエ級数で表すと、
![Rendered by QuickLaTeX.com \begin{eqnarray*} f(x)=x&=&2\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n}\sin nx\\\\ &=&2\left[ \sin x - \frac{\sin 2x}{2}+\frac{\sin 3x}{3}-\cdots \right] \quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-11286eff904a106c57c57f1104714523_l3.png)
次に、
![]()
を求める。
上で求めたフーリエ級数について、![]() と置くと、
と置くと、
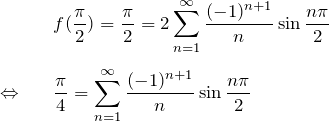
ここで右辺を計算する。![]() の値は
の値は ![]() に対して、
に対して、![]() となる。よって、
となる。よって、
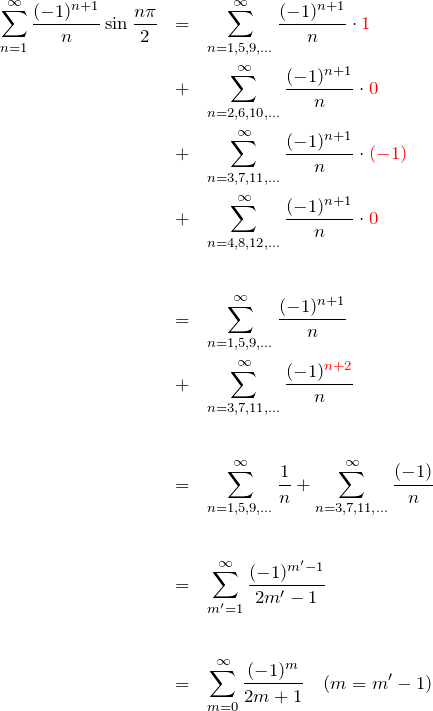
以上より、
![]()
おまけ:
最後の結果、
![]()
はライプニッツ級数として円周率 ![]() の近似を求めるのに使われた。プラスとマイナスを交互に足しているため、振動しながら
の近似を求めるのに使われた。プラスとマイナスを交互に足しているため、振動しながら ![]() に近づく。
に近づく。