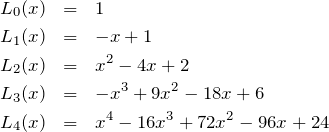水素原子の動径方向の波動関数を求めるときに使われる、ラゲール(Laguerre)多項式などをまとめる。証明付きでよく使う式もまとめた。
また、ラゲール多項式 ![]() のみで数式が多くなったので、ラゲール陪多項式とラゲール関数については別に扱う。
のみで数式が多くなったので、ラゲール陪多項式とラゲール関数については別に扱う。
目次
ラゲール多項式と陪多項式の注意
おもに、ラゲール多項式 ![]() とラゲール陪多項式
とラゲール陪多項式 ![]() について学ぶ。
について学ぶ。 ![]() の肩に
の肩に ![]() があるかどうか注意しておく。ただし、
があるかどうか注意しておく。ただし、![]() の関係は一応ある。
の関係は一応ある。 ![]() の有無は、微分方程式の中に
の有無は、微分方程式の中に ![]() が入っているかどうかでわかる。
が入っているかどうかでわかる。
以下では、微分方程式とラゲール多項式について簡単にまとめた。
ラゲールの微分方程式
ラゲール多項式を導くラゲールの微分方程式
ラゲールの微分方程式は
![]()
の形をしている。![]() は
は ![]() の整数のとき解が存在することが知られており、そのひとつの解はラゲール多項式
の整数のとき解が存在することが知られており、そのひとつの解はラゲール多項式 ![]() によって表される。
によって表される。
ラゲール陪多項式を導く微分方程式
次にラゲールの陪多項式に関する微分方程式をつくる。 ![]() として、上の微分方程式を
として、上の微分方程式を ![]() について
について ![]() 回微分すると、左辺は
回微分すると、左辺は
![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{d^m}{dx^m}\left[x\frac{d^2y}{dx^2}+(1-x)\frac{dy}{dx}+n y\right] &=&\textcolor{blue}{\frac{d^m}{dx^m}\left(x\frac{d^2y}{dx^2}\right)} +\textcolor{red}{\frac{d^m}{dx^m}\left((1-x)\frac{dy}{dx}\right)}+n\frac{d^m y}{dx^m} \\ &=&\textcolor{blue}{m\frac{d^{m+1}y}{dx^{m+1}}+x\frac{d^{m+2}y}{dx^{m+2}}}\\ &&\quad\textcolor{red}{-m\frac{d^{m}y}{dx^{m}}+(1-x)\frac{d^{m+1}y}{dx^{m+1}}}\\ &&\quad\quad+n\frac{d^m y}{dx^m}\\ &=& x\frac{d^{m+2}y}{dx^{m+2}}+(m+1-x)\frac{d^{m+1}y}{dx^{m+1}}+(n-m)\frac{d^m y}{dx^m} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-f7db73ee45f1787081af2d4c8405c276_l3.png)
式変形の途中、合成関数の![]() 回微分を実行するときにライプニッツの定理(「二項定理の微分版」のようなもの)
回微分を実行するときにライプニッツの定理(「二項定理の微分版」のようなもの)
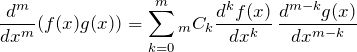
を用いた。
得られた微分方程式
![]()
において ![]() とすると、
とすると、
![]()
となる。微分方程式(d2′)の解の一つはラゲール陪多項式 ![]() になる。微分方程式に
になる。微分方程式に ![]() が含まれるため、多項式は
が含まれるため、多項式は ![]() の添え字をもつ。 陪多項式とラゲール多項式
の添え字をもつ。 陪多項式とラゲール多項式 ![]() の関係は
の関係は
![]()
である。
以下、微分方程式(d2)の解のひとつが ![]() になることを示す。
になることを示す。
微分方程式(d1)の解がラゲール多項式
![]()
が成り立つ。これを
![]()
となる。
![]()
と置けば、式(d3)より、
![]()
となる。したがって、
*これらの微分方程式はステュルム-リウヴィル型微分方程式に含まれる。
ラゲール多項式の諸性質と証明
ラゲール多項式 ![]() はラゲールの微分方程式を満たすである。
はラゲールの微分方程式を満たすである。
![]()
母関数
母関数は
![]()
となる。
多項式展開
母関数を使って
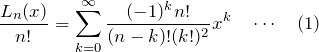
のように多項式展開できる。ここで、![]() についての和は
についての和は ![]() の代わりに
の代わりに ![]() でも良い。なぜなら
でも良い。なぜなら ![]() で
で
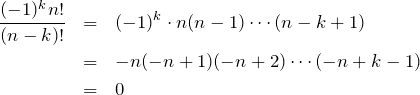
となるためである(因数が![]() 個あるため)。
個あるため)。
(*)より
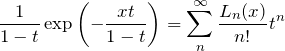
である。左辺を展開して
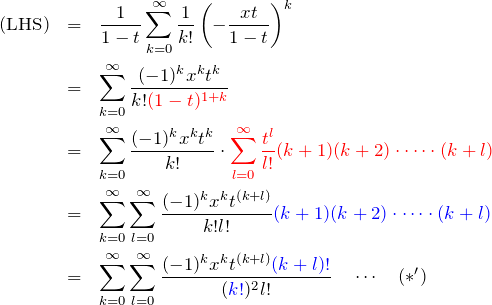
ここで、
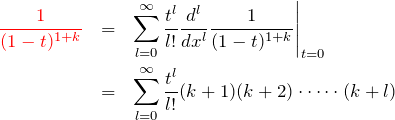
と
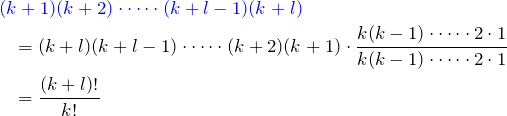
を利用した。
得られた(*)と(*’)から
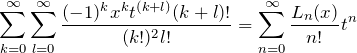
となる。
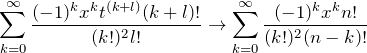
となる(
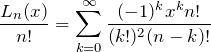
となる。
便利な式
上の ![]() の多項式展開を利用して
の多項式展開を利用して
![]()
が得られる。
左辺から右辺を導く。合成関数の微分については、上述したライプニッツの定理を利用する。 最後に上で求めた
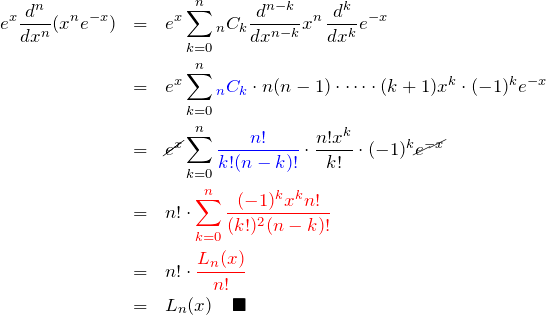
上で説明したように、
直交性、正規直交基底の導入
![]()
は正規直交基底をなす。つまり、
![]()
となる。![]() については直交基底である。つまり
については直交基底である。つまり
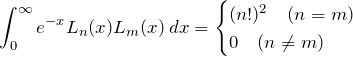
である(規格化はされていない)。
以下では ![]() が直交系をなし、
が直交系をなし、![]() が正規直交していることを示す。 基本的に式(2)を用いて、部分積分を複数回実行する。また、
が正規直交していることを示す。 基本的に式(2)を用いて、部分積分を複数回実行する。また、![]() としても一般性は失われない。
としても一般性は失われない。
![]()
としていく。
合成関数の微分に注意しながら計算を進める。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_0^\infty e^{-x}L_m(x)L_n(x)\, dx &=& \int_0^\infty e^x \frac{d^m}{dx^m}\left(x^m e^{-x}\right) \frac{d^n}{dx^n}\left(x^ne^{-x}\right)\,dx\\ &=& \cancelto{0}{\left[ e^x \frac{d^m}{dx^m}(x^me^{-x})\frac{d^{\textcolor{blue}{n-1}}}{dx^{\textcolor{blue}{n-1}}}(x^ne^{-x}) \right]_0^\infty}\\ &&\quad-\int_0^\infty \textcolor{red}{\frac{d}{dx}}\left( e^x\frac{d^m}{dx^m}(x^me^{-x}) \right) \frac{d^{\textcolor{blue}{n-1}}}{dx^{\textcolor{blue}{n-1}}}(x^ne^{-x})\,dx\\ &=& -\int_0^\infty e^x\left( \frac{d^m}{dx^m}+\frac{d^{m+1}}{dx^{m+1}} \right)(x^me^{-x})\frac{d^{n-1}}{dx^{n-1}}(x^ne^{-x})\,dx\\ &=&-\cancelto{0}{\left[ e^x \frac{d^m}{dx^m}(x^me^{-x})\frac{d^{\textcolor{blue}{n-2}}}{dx^{\textcolor{blue}{n-2}}}(x^ne^{-x}) \right]_0^\infty}\\ &&\quad+\int_0^\infty e^x\left( \frac{d^m}{dx^m}+\textcolor{red}{2}\frac{d^{m+1}}{dx^{m+1}}+\frac{d^{m+2}}{dx^{m+2}} \right)\frac{d^m}{dx^m}(x^me^{-x}) \frac{d^{\textcolor{blue}{n-2}}}{dx^{\textcolor{blue}{n-2}}}(x^ne^{-x})\,dx\\ &=&\cdots\\ &=& (-1)^n\int_0^\infty \cancel{e^x}\left( \frac{d^m}{dx^m}+\textcolor{red}{n}\frac{d^{m+1}}{dx^{m+1}}+\cdots+\frac{d^{m+n}}{dx^{m+n}} \right)(x^me^{-x})\cdot x^n \cancel{e^{-x}}\,dx\\ &=&(-1)^n\int_0^\infty x^n\sum_{k=0}^n {}_nC_k \frac{d^{m+k}}{dx^{m+k}}(x^me^{-x}) \,dx\\ &=&(-1)^n \sum_{k=0}^n {}_nC_k \int_0^\infty x^n\frac{d^{m+k}}{dx^{m+k}}(x^me^{-x}) \,dx \quad\cdots\quad(3) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-c97e51f1123dbbabadb35166165a5d53_l3.png)
つぎに、最後の行の積分を
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\int_0^\infty x^n\frac{d^{m+k}}{dx^{m+k}}(x^me^{-x}) \,dx\\ &&\quad= \cancelto{0}{\left[x^n\frac{d^{m+k-1}}{dx^{m+k-1}}(x^me^{-x})\right]_0^\infty} -\int_0^\infty n x^{n-1} \frac{d^{m+k-1}}{dx^{m+k-1}}(x^me^{-1})\, dx\\ &&\quad=\cdots\\ &&\quad =(-1)^n n!\int_0^\infty \frac{d^{m+k-n}}{dx^{m+k-n}}(x^me^{-x})\, dx \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-96c98cf1938448836418ee1269881606_l3.png)
これを式(3)へ代入して、
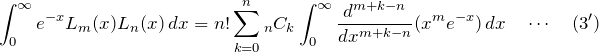
となる。
つぎにこの積分を実行する。簡単のため
![]()
の振る舞いをみる。
![Rendered by QuickLaTeX.com \begin{eqnarray*} I_{l,m}&=&\int_0^\infty \textcolor{red}{\frac{d}{dx}}\,\frac{d^{l-1}}{dx^{l-1}}(x^m e^{-x})\, dx\\ &=&\left[ \frac{d^{l-1}}{dx^{l-1}}(x^me^{-x}) \right]_0^\infty\\ &=&\left[ \left( Ax^{m-l+1}+Bx^{m-l+2}+\cdots \right)e^{-x} \right]_0^\infty\\ &=&\left[ \left( Ax^{m-l}+Bx^{m-l+1}+\cdots \right)\textcolor{blue}{xe^{-x}} \right]_0^\infty\\ &=&0 \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-56e27e74cc3ea967920c8c8e250541ea_l3.png)
ここで、
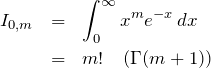
となる。積分はガンマ関数
(i)(ii)の結果をまとめて
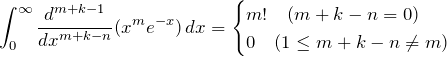
となる。
![]()
であり、
したがって
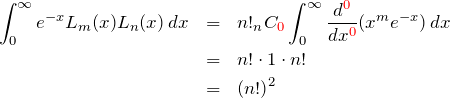
これより、
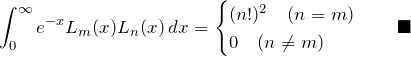
また、
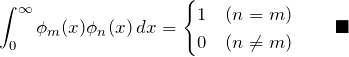
はじめの5項の値
はじめの5つ程度の項を具体的に書いておく。
![]()
を用いて簡単に求めることができる。