全記事一覧 > 数学 > フーリエ変換／ラプラス変換

【フーリエ変換】フーリエ積分に現れる {exp(ikx)} の直交性

　フーリエ積分（フーリエ変換）に現れる e^{ikx} に関して、 その以下の直交性を示さなくてはならない。 少々、テクニカルだが覚えておきたい。

直交性

    \begin{eqnarray*} \frac{1}{2\pi}\int_{-\infty}^{\infty}e^{i(k-k')x}\,dx=\delta(k-k') \end{eqnarray*}


直交性の証明

　ここでの基底は\{\frac{1}{\sqrt{2\pi}}e^{ikx}\}のように \frac{1}{\sqrt{2\pi}}倍したものを用いる。


    \begin{eqnarray*} \frac{1}{2\pi}\int_{-\infty}^{\infty}e^{i(k-k')x}\,dx \end{eqnarray*}

　では扱いにくいため、積分区間を変えよう。

    \begin{eqnarray*} \frac{1}{2\pi}\int_{-L}^{L}e^{i(k-k')x}\,dx \end{eqnarray*}

　あとで、L\to\inftyと取れば良い。


　この積分を単純に計算していく

    \begin{eqnarray*} \frac{1}{2\pi}\int_{-L}^{L}e^{i(k-k')x}\,dx &=&\frac{1}{2\pi}\left[\frac{e^{i(k-k')x}}{i(k-k')}\right]_{-L}^{L}\\\\ &=&\frac{1}{2\pi}\cdot\frac{e^{i(k-k')L}-e^{-i(k-k')L}}{i(k-k')}\\\\ &=&\frac{1}{\pi}\cdot\frac{\sin L(k-k')}{(k-k')}\quad(\because\sin \theta=\frac{e^{i\theta}-e^{-i\theta}}{2i})\\\\ &\to&\delta(k-k')\quad({L\to\infty})\quad\blacksquare \end{eqnarray*}

最後の等号については「補足」を参考にされたい。 この結果から基底は\{\frac{1}{\sqrt{2\pi}}e^{ikx}\}は直交する。


*いま、考えているkは連続であるため 直交性はデルタ関数\delta(k-k')によって表されている。 複素フーリエ級数のような離散的なkを扱っている場合は クロネッカーのデルタ\delta_{nm}に置き換わることにも注意する。

**いまの基底の取り方（\frac{1}{\sqrt{2\pi}}因子つき）では kに関する積分でも規格直交している。

    \begin{eqnarray*} \frac{1}{2\pi}\int_{-\infty}^{\infty}e^{ik(x-x')}\,dk=\delta(x-x') \end{eqnarray*}


簡単な補足：デルタ関数

　上式の最後の行でデルタ関数の定義の１つとして以下の極限

    \begin{eqnarray*} \delta(x)=\frac{1}{\pi}\,\lim_{u\to\infty}\,\frac{\sin ux}{x} \end{eqnarray*}

を用いた（図を参照）。


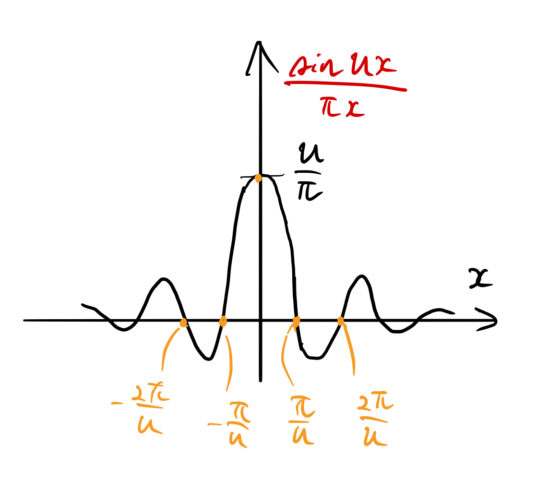
この右辺がデルタ関数の定義

    \begin{eqnarray*} \int_{-\infty}^{+\infty}\delta(x)\,dx=1 \end{eqnarray*}

を満たすことは、実際に計算してみればわかる。


    \begin{eqnarray*} \int_{-\infty}^{+\infty} \frac{1}{\pi}\,\lim_{u\to\infty}\,\frac{\sin ux}{x}\,dx &=& \frac{1}{\pi}\int_{-\infty}^{+\infty}\lim_{u\to\infty}\,\frac{\sin ux}{\textcolor{blue}{u}x}\,\textcolor{blue}{u}dx\\\\ &=& \frac{1}{\pi}\int_{-\infty}^{+\infty}\,\frac{\sin x'}{x'}\,dx'\quad(x'=ux;\,dx'=udx)\\\\ &=& \frac{1}{\pi}\cdot\pi\\\\ &=&1\quad\blacksquare \end{eqnarray*}

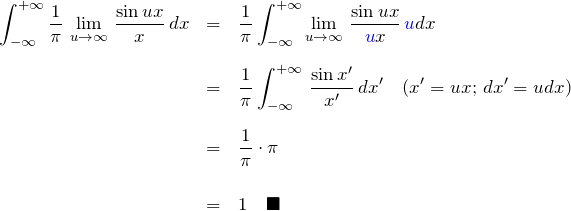
となり、確かにデルタ関数の定義を満たす。


*最後の積分には、以下のディリクレ積分を利用した。

    \begin{eqnarray*} \int_0^{\infty}\frac{\sin x}{x}\,dx=\frac{\pi}{2} \end{eqnarray*}

　この積分は、複素積分を利用することで解くことができる。


まとめ

　 \inftyが入ると途端に取り扱いが難しくなる。 ここでもややテクニカルな手法を用いているため注意したい。

　得られた結果自体はよく知られた重要なものである。



コメントを残す

メールアドレスが公開されることはありません。