双極子モーメントの外場中でのポテンシャルエネルギーを考える。ここでは、導出にはトルク ![]() は用いない。電場中の電気双極子モーメントでも、磁場中の磁気双極子モーメントでも同じ形になる。
は用いない。電場中の電気双極子モーメントでも、磁場中の磁気双極子モーメントでも同じ形になる。
外場 ![]() 中にある双極子モーメント
中にある双極子モーメント ![]() のポテンシャルは以下で与えられる。
のポテンシャルは以下で与えられる。
![]()
1. トルクを使わない導出
図のように電場 ![]() から傾いた電気双極子モーメント
から傾いた電気双極子モーメント ![]() のポテンシャルは、
のポテンシャルは、![]() と
と ![]() の内積の逆符号である。
の内積の逆符号である。
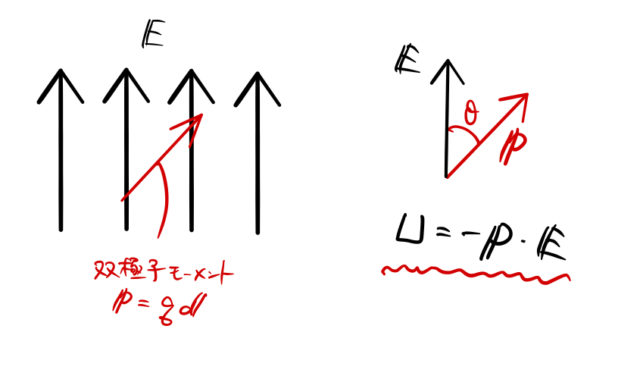
以下では ![]() を導出しよう。
を導出しよう。
1.1 無限遠から運んでくる
簡単に言って、電気双極子モーメントは ![]() の点電荷と
の点電荷と ![]() の点電荷のペア である。点電荷は無限遠でポテンシャルを 0 に定義していることを思い出そう。
の点電荷のペア である。点電荷は無限遠でポテンシャルを 0 に定義していることを思い出そう。
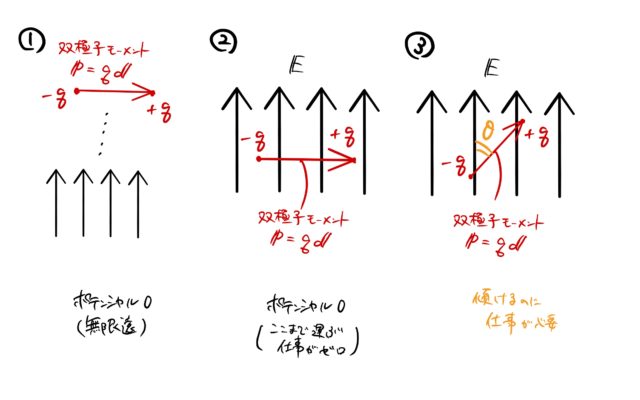
最終的に③の状態になるまでどれだけ仕事したか、を考える。
①:無限遠にある双極子モーメント(2つの点電荷)、ポテンシャルは無限遠を 0 にとる。
②:無限遠から原点まで運んでくる。点電荷は電場から ![]() の静電気力を電場方向
の静電気力を電場方向 ![]() に受ける。
に受ける。
- 電場に垂直な方向:仕事ゼロ
- 電場と並行な方向:
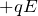 と
と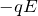 の仕事は逆符号で相殺してゼロ
の仕事は逆符号で相殺してゼロ
したがって、電場と垂直な双極子モーメントをポテンシャル 0(基準) として、電場方向に双極子モーメントを傾けていく。
③:電場と双極子モーメントのなす角が ![]() の状態(目的の状態)
の状態(目的の状態)
1.2 双極子モーメントを傾ける
図に全部描いてしまったが。双極子モーメントは赤矢印で ![]() で表されている(
で表されている(![]() )。
)。
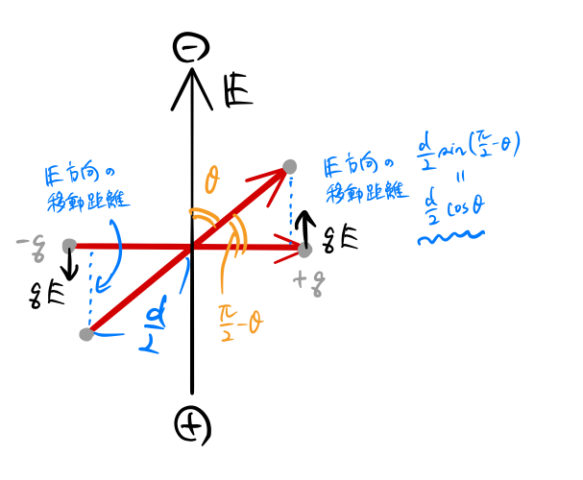
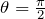 をポテンシャル 0 とする。
をポテンシャル 0 とする。- 双極子モーメント:赤矢印、両端に
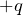 と
と 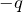 の点電荷、双極子モーメントの中点(
の点電荷、双極子モーメントの中点( )を軸に回転
)を軸に回転 - 電場
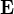 により2つの点電荷はそれぞれ逆方向に力
により2つの点電荷はそれぞれ逆方向に力 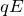 を受ける
を受ける - 電場方向の電荷の移動距離は

- 電場垂直方向の移動については仕事 0
したがって電場 ![]() にある 電気双極子モーメント
にある 電気双極子モーメント ![]() のポテンシャルは、
のポテンシャルは、
![Rendered by QuickLaTeX.com \begin{eqnarray*} U&=&2\left[\textcolor{red}{-}qE\cdot\frac{d}{2}\cos\theta\right]\\ \\ &=& \textcolor{red}{-}qdE\cos\theta \\ \\ &=& \textcolor{red}{-}{\bf p}\cdot {\bf E} \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-00980b50ab1b89685a919a8f477cf4c3_l3.png)
なぜマイナスになったかわからない場合は重力の位置エネルギーを考えてみるとよい。次にその説明をする。
1.3 なぜマイナスがついた?
保存力である重力の位置エネルギーは高さ ![]() として
として ![]() になる。
になる。
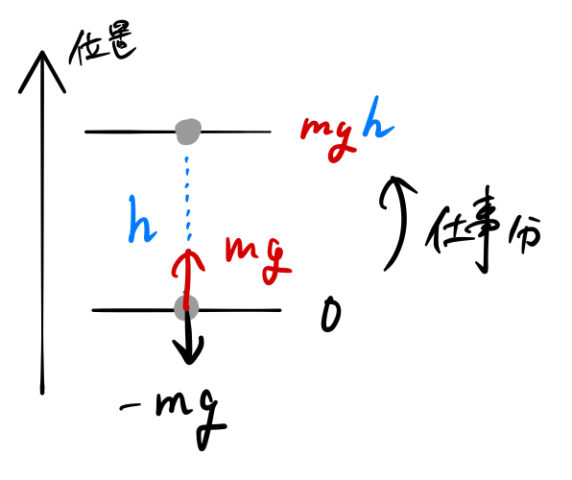
基準 ![]() の位置から高さ
の位置から高さ ![]() まで質量
まで質量 ![]() の物体を運ぶとき、重力は常に下向きの負(
の物体を運ぶとき、重力は常に下向きの負(![]() )になっている。高さ
)になっている。高さ ![]() まで物体を運ぶと、重力と同じ上向きの力
まで物体を運ぶと、重力と同じ上向きの力 ![]() による仕事
による仕事 ![]() が必要になる。
が必要になる。
したがって、位置エネルギーは ![]() となる。
となる。
これとまったく同じように、![]() の電荷も
の電荷も ![]() と逆向きの力(図の下向き)
と逆向きの力(図の下向き) ![]() によって図の上向きに運ばれている。したがって、最終状態にある
によって図の上向きに運ばれている。したがって、最終状態にある ![]() の電荷のポテンシャルエネルギーは、
の電荷のポテンシャルエネルギーは、
(力: ![]() ) × (移動距離
) × (移動距離 ![]() )
)
となる。![]() の電荷についても考えるので、2倍してやれば良い。
の電荷についても考えるので、2倍してやれば良い。
2. まとめ
電気双極子モーメントを考えたが、磁気双極子モーメントの場合も同様である。
![]()
双極子モーメントと外場の内積の形になっているため、双極子モーメントと外場の向きが同じならエネルギー的に安定である。したがって、磁気モーメントの場合は、外部磁場によってモーメントは外部磁場方向に揃おうとする(常磁性体を思い浮かべれば良い)。