おもに固体の体積膨張率/等温圧縮率/体積弾性率を見ていく。
体積膨張率
定義:体積で表す
![]()
体積膨張率 ![]() は、圧力一定下において熱を加えたときに物体の体積がどれくらいの割合で大きくなるかを表す(熱膨張)。 体積膨張率は線膨張率と同じ、熱膨張率のひとつである。
は、圧力一定下において熱を加えたときに物体の体積がどれくらいの割合で大きくなるかを表す(熱膨張)。 体積膨張率は線膨張率と同じ、熱膨張率のひとつである。
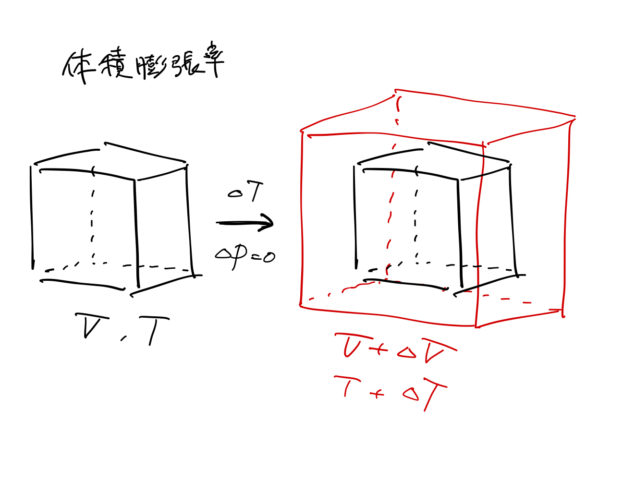
状態方程式によると ![]() (理想気体で
(理想気体で ![]() )であり、体積は圧力と温度の関数になる。 定圧
)であり、体積は圧力と温度の関数になる。 定圧 ![]() (または、
(または、![]() )のときの体積変化を考える。 体積膨張率は、
)のときの体積変化を考える。 体積膨張率は、![]() の状態から温度
の状態から温度 ![]() 、体積
、体積 ![]() となったときに、単位温度あたり
となったときに、単位温度あたり
![]()
の割合で体積が変化したことから求めることができる(割合なので ![]() が付く)。
が付く)。
理想気体を考えれば、熱を加えて温度を上げていけば体積が膨張することは直感的にもわかる。
固体の場合も同様に、高温ほど体積は膨張する傾向にあり、そのとき![]() である。
というのも、原子の振動(格子振動)が激しくなるためである。
である。
というのも、原子の振動(格子振動)が激しくなるためである。
しかしながら、必ずしも温度が上がれば膨張するわけではない。 熱を加えると体積が減少するような、![]() となるような材料も存在する。 身近なところで、水の密度が4℃で最大であることが知られており、4℃以下で冷却に伴って体積は膨張する。 また個体などで熱膨張率が低いものとして、Fe-Ni系などはインバー合金として知られている
となるような材料も存在する。 身近なところで、水の密度が4℃で最大であることが知られており、4℃以下で冷却に伴って体積は膨張する。 また個体などで熱膨張率が低いものとして、Fe-Ni系などはインバー合金として知られている![]() 。
。
* インバー合金(Invar Alloy)のinvarは、不変を意味するinvariantから来ている。 この合金はギヨームにより研究され、1920年にノーベル物理学賞を受賞している。また翌年1921年にはアインシュタインがノーベル賞を受賞している。
密度で表す
流体などの場合は密度
![]()
により、
![]()
だから、
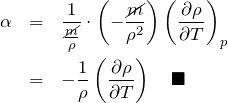
となる。
理想気体の体積膨張率
![]() モル理想気体の状態方程式の
モル理想気体の状態方程式の
![]()
および、分子量 ![]() と密度
と密度 ![]() で表した
で表した
![]()
から体積膨張率 ![]() は
は
![]()
等温圧縮率
定義
![]()
等温圧縮率(Complesibility)は、圧縮のしやすさを表す。 右辺のマイナスは、「圧力の増加に対して、体積が減少する」割合を正とするためである。 式の意味は体積膨張率と同じように考えればよい。
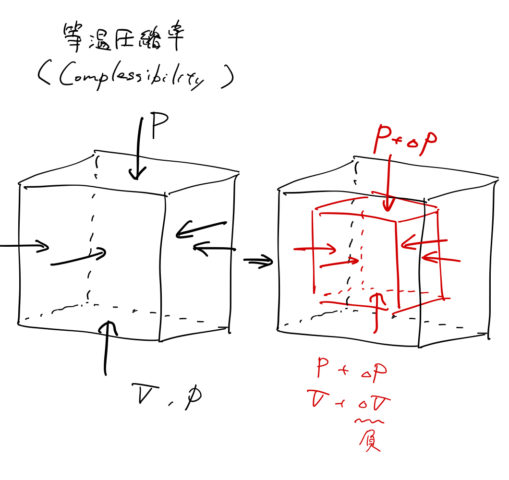
図は等温(![]() )での圧縮(
)での圧縮(![]() )を表している。 圧縮により状態は
)を表している。 圧縮により状態は ![]() となる。 したがって、圧力あたりの体積減少の割合は
となる。 したがって、圧力あたりの体積減少の割合は
![]()
となる。
式から分かるように、![]() が大きければ、圧力に対して体積変化が大きくなる。すなわち、圧縮しやすい。
が大きければ、圧力に対して体積変化が大きくなる。すなわち、圧縮しやすい。
![]() が大きく圧縮しやすいことは、固体中の原子がバネでつながっているモデルで考えると、バネ定数
が大きく圧縮しやすいことは、固体中の原子がバネでつながっているモデルで考えると、バネ定数 ![]() が小さいことに対応する
が小さいことに対応する![]() 。
。
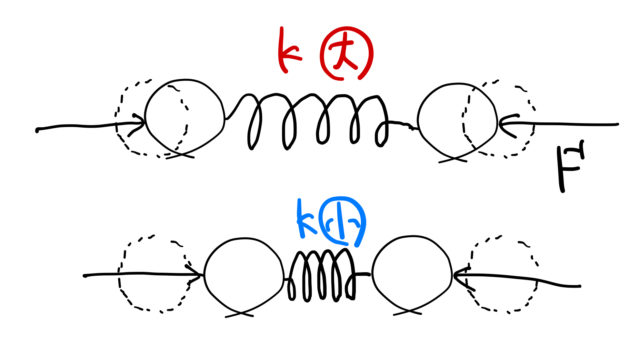
* 1次元のバネ定数 ![]() をそのまま3次元で考えるのはあまりに単純なので、体積弾性率
をそのまま3次元で考えるのはあまりに単純なので、体積弾性率 ![]() を考える。
を考える。
理想気体の等温圧縮率
![]() モルの理想気体については、
モルの理想気体については、![]() から
から
![]()
より、
![]()
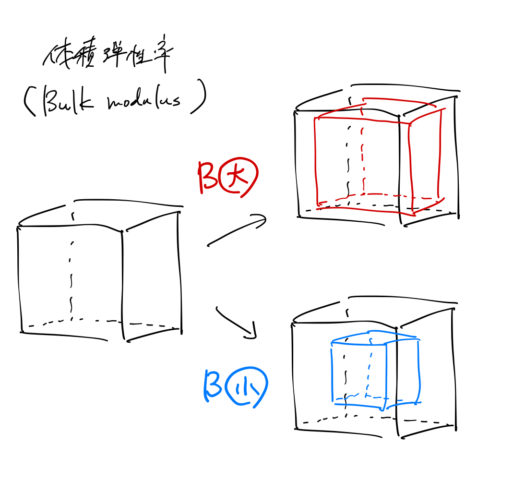
体積弾性率
定義
圧縮率 ![]() の逆数をとって
の逆数をとって
![]()
3次元的なバネのバネ定数のイメージで、![]() が大きければ圧縮しにくく、
が大きければ圧縮しにくく、![]() が小さければ圧縮しやすい。
が小さければ圧縮しやすい。
体積膨張率αとの関係
![]()
これを導く。 まず、状態方程式から ![]() である。
である。![]() は圧力を
は圧力を ![]() で表したもので、理想気体のときは
で表したもので、理想気体のときは ![]() である。
である。 ![]() が
が ![]() の関数であるため、
の関数であるため、![]() の変化
の変化 ![]() は体積変化
は体積変化 ![]() と 温度変化
と 温度変化 ![]() に関係する。 一般に、
に関係する。 一般に、
![]()
となる![]() 。 また
。 また ![]() とも書けるため、
とも書けるため、
![]()
である。式(2)を式(1)へ代入して、![]() の項に分ける。
の項に分ける。
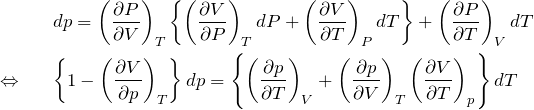
等圧変化のとき ![]() より、右辺のカッコ内がゼロになる(
より、右辺のカッコ内がゼロになる(![]() )。
)。
![]()
ここで、体積膨張率 ![]() と体積弾性率
と体積弾性率 ![]() の定義から
の定義から
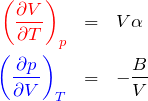
を用いて、
![]()
を得る。
* ![]() ,
, ![]() の状態変化に対して
の状態変化に対して ![]() はテイラー展開により
はテイラー展開により
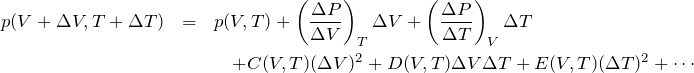
となる(![]() は
は ![]() の関数)。2次以上の項を無視して、圧力
の関数)。2次以上の項を無視して、圧力 ![]() の全微分の形
の全微分の形 ![]() を得る(2変数関数の微分などを参照)。
を得る(2変数関数の微分などを参照)。