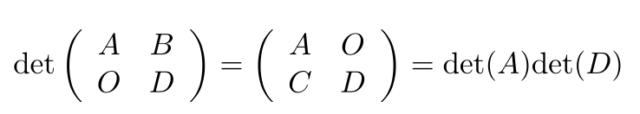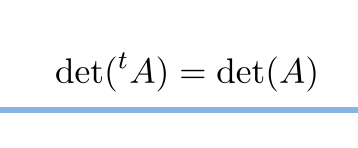![]() の行列
の行列![]() について、
について、
![]() の固有値を
の固有値を![]() (i=1, 2, …, n)とすると
(i=1, 2, …, n)とすると
![Rendered by QuickLaTeX.com \[ {\rm tr}A =\sum_{i=1}^{n} \lambda_i \]](https://batapara.com/wp-content/ql-cache/quicklatex.com-47c4dd9ffc1984a23e4d806571d100b0_l3.png)
が成立することを示す。(tr(![]() )=tr(
)=tr(![]() )は使わない。)
)は使わない。)
この式は行列のトレースと固有値を結ぶ関係式となっている。
まず
固有多項式 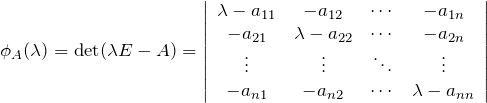
は、 ![]() とおける。
とおける。
実際に係数![]() を求めてみる。すなわち
を求めてみる。すなわち![]() の係数を求める。
の係数を求める。
はじめに、行列式の第1列に対する余因子展開を考える。
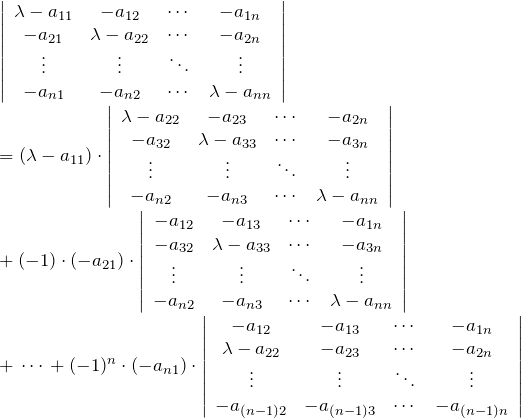
余因子展開により![]() 行列の行列式が、
行列の行列式が、
![]() 行列の行列式の和で表された。
行列の行列式の和で表された。
第2項以下について行列式の![]() は次数は高々(n-2)次である。
は次数は高々(n-2)次である。
つまり、第1項からのみ![]() が現れる。
が現れる。
具体的には、![]() からのみ現れ、
からのみ現れ、
(1) ![]()
と表される。
一方で、固有多項式![]() は、
は、
![]()
なので、
(2) ![Rendered by QuickLaTeX.com \[\alpha_1=-(\lambda_1+\lambda_2 \cdots \lambda_n)=\sum_{i=1}^{n} \lambda_i \]](https://batapara.com/wp-content/ql-cache/quicklatex.com-76e5b85cf8d2d3769f4ba07753b45344_l3.png)
となる。
(1)(2)より ![]() が証明された。
が証明された。