演算子が指数関数の肩に乗っていることがある。実は指数関数の展開により簡単に表されることを学び、ここでは、量子統計力学で重要となる以下の式を示そう。![]() はハミルトニアンを表す。
はハミルトニアンを表す。![]() はハミルトニアンの固有値エネルギーを表している。
はハミルトニアンの固有値エネルギーを表している。
分配関数とトレース(Tr)の関係【統計量子力学】
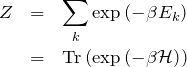
1. 1つ目の等号
一つ目の等号については、分配関数 ![]() で状態和を表す。分配関数の意味がわからない場合は、以下の記事を参考にすると良い。
で状態和を表す。分配関数の意味がわからない場合は、以下の記事を参考にすると良い。
2. 2つ目の等号
とくにここでは二つ目の等号について証明していく。
![]()
を示す。あるユニタリ行列 ![]() により ハミルトニアン
により ハミルトニアン![]() が対角化されるとする。すなわち、
が対角化されるとする。すなわち、
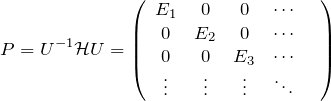
のように対角要素にエネルギー固有値 ![]() が並ぶ。ここで行列の次元は無限次元であるとする(
が並ぶ。ここで行列の次元は無限次元であるとする(![]() 次元であっても証明は変わらない。)対角化行列
次元であっても証明は変わらない。)対角化行列 ![]() に対して、
に対して、
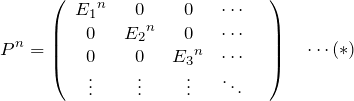
2.1 指数関数の展開
![]() を展開する。
を展開する。
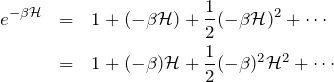
のように展開できる。
指数関数の肩に演算子がある場合の展開
実数関数の 指数関数(exponential function)の展開
![]()
と同様に、演算子 ![]() に対して、
に対して、
![]()
ここで、
![Rendered by QuickLaTeX.com \begin{eqnarray*}U^{-1}e^{-\beta{\mathcal H}}U&=&U^{-1}\left[ {\bf 1}+(-\beta){\mathcal H}+\frac{1}{2}(-\beta)^2{\mathcal H}^2+\cdots \right] U\\ \\&=&U^{-1}{\bf 1}U+(-\beta)U^{-1}{\mathcal H}U+\frac{1}{2}(-\beta)^2 U^{-1}{\mathcal H}^2U+\cdots \\\\&=&U^{-1}U+(-\beta)U^{-1}{\mathcal H}U+\frac{1}{2}(-\beta)^2 U^{-1}{\mathcal H}U\cdot U^{-1}{\mathcal H}U+\cdots \\&& \quad \quad \quad (\because UU^{-1}=U^{-1}U=1)\\ \\&=&{\bf 1}+(-\beta)P+\frac{\beta^2}{2}P^2+\cdots \\ \\&=&\left( \begin{array}{cccccc}1-\beta E_1 +\frac{\beta^2}{2}{E_1}^2 \cdots& 0 & 0 &\cdots \\0 &1-\beta E_2 +\frac{\beta^2}{2}{E_2}^2 \cdots& 0 & \cdots \\0 & 0 & 1-\beta E_3 +\frac{\beta^2}{2}{E_3}^2 \cdots & \cdots \\\vdots &\vdots &\vdots & \ddots &\end{array} \right)\\ \\&=&\left( \begin{array}{cccccc}e^{-\beta E_1} \cdots& 0 & 0 &\cdots \\0 &e^{-\beta E_2} \cdots& 0 & \cdots \\0 & 0 & e^{-\beta E_3} \cdots & \cdots \\\vdots &\vdots &\vdots & \ddots &\end{array} \right)\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-eff42d1e6d3dcf9fb505dc6457f59c7a_l3.png)
であるので、両辺のトレース(Tr)をとることで
![]()
である。最後にトレースの巡回性、
![]()
により、![]() として、
として、
![]()
となる。 ![]()
分配関数とトレース
![]()
3. まとめ
この式は重要なので覚えておく。
[U,H]=0は誤りではないでしょうか。
これが正しいとすると、
P=U^{-1} HU=U ^{-1} UH=H,
となるので、ハミルトニアンHを初めから対角化された基底で考えていることになります。このとき、Uは恒等演算子(単位行列)になります。
Tr(U^{-1}e^{-\beta H} U)=Tr(e^{-\beta H})
はトレースの巡回性
Tr(AB)=Tr(BA),
より得られます。
失礼いたしました。勝手に交換すると仮定してしまいました。
ご指摘ありがとうございます。