電磁気学でよく目にする以下のポアソン方程式を解いていこう。 この式は偏微分方程式であり、「グリーン関数」なるもので解くことができる。
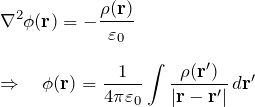
目次
1. Green関数を使った解法の概要
微分方程式をGreen関数によって解く。 その一般的な解き方の詳細と構造については、「Green関数の簡単な意味(基礎)」に書いた。 その概要は、
「微分方程式を解いて![]() を求める」
を求める」
という問題を
「Green関数の満たすべき方程式を解いてGreen関数を求める」
という問題に置き換えることである。 今の場合、
![]()
に対して、Green関数が満たすべき方程式は
![]()
である。右辺はデルタ関数。
(*)’により![]() が求まれば、
が求まれば、
![]()
が(*)の解になる。
実際、(*)の左辺は
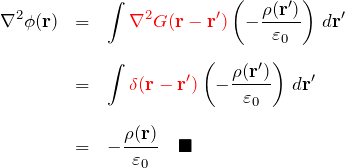
となり、右辺に一致する。
2. ポアソン方程式を解く
元々の微分方程式を直接解いてスカラーポテンシャルを求める代わりに、Green関数を求めればよいことがわかった。 ここでは以下の手順でGreen関数を求めていく。
- Green関数が満たす式を作る
- その式を解くためにフーリエ変換を利用する
- 積分するために球座標に変換する
Green関数が満たす式
まず、Green関数![]() が満たす方程式は以下の通り。
が満たす方程式は以下の通り。
![]()
この ![]() が分かれば、
が分かれば、![]() が分かることは上で述べた通りである。
が分かることは上で述べた通りである。
解くためのフーリエ変換
式(*)”を解くためにフーリエ変換を行う。![]() は3次元であるため、 フーリエ変換も各
は3次元であるため、 フーリエ変換も各![]() について行う。 (よくわからない場合は、フーリエ変換の意味はあまり考えなくて良い。とにかく定義通り計算していこう。)
について行う。 (よくわからない場合は、フーリエ変換の意味はあまり考えなくて良い。とにかく定義通り計算していこう。)
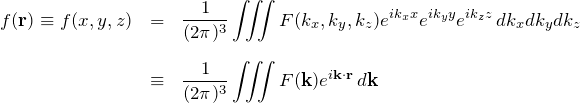
今の場合、
左辺の![]() のフーリエ変換:
のフーリエ変換:
![]()
右辺の![]() のフーリエ変換:
のフーリエ変換:
![]()
(デルタ関数のフーリエ変換が1になることを思い出す。)
したがって、式(*)”は、
![]()
となる。
この左辺を計算していこう。まず、![]() は
は ![]() のように
のように![]() に作用し、
に作用し、![]() には作用しないことに注意する。
には作用しないことに注意する。
![]() について計算する。
について計算する。
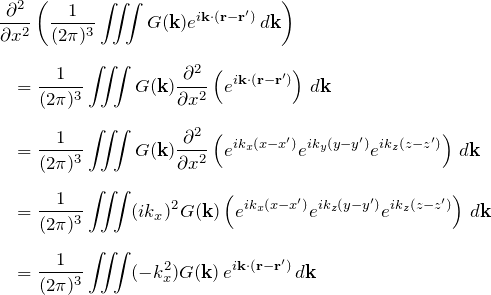
![]() も同様に
も同様に
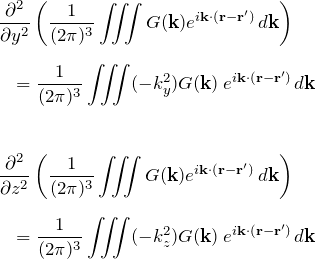
以上より
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\nabla^2\left(\frac{1}{(2\pi)^3}\iiint G({\bfk})e^{i{\bfk}\cdot{(\bfr-\bfr')}}\,d{\bfk}\right)\\\\ &&\quad= \frac{1}{(2\pi)^3}\iiint\left[-(k_x^2+k_y^2+k_z^2)\right]G({\bfk})\,e^{i{\bfk}\cdot{(\bfr-\bfr')}}\,d{\bfk} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-6da3cf25b4a390b4496e1de7a884f646_l3.png)
となる。よって式(*)”は
![]()
被積分関数を等しいとして、
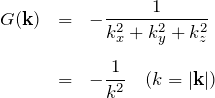
となる。これでGreen関数のフーリエ成分(![]() 成分)が求まったので、
逆フーリエ変換(式(**))により
成分)が求まったので、
逆フーリエ変換(式(**))により
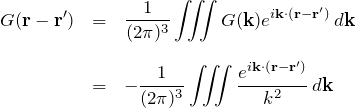
となる。あとは最後の積分を計算してやれば良い。
積分のための球座標変換
3次元の直交座標(![]() )における積分は、以下の球座標(極座標)に変換すると計算しやすい。
)における積分は、以下の球座標(極座標)に変換すると計算しやすい。
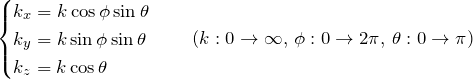
![]() である。
である。 ![]() ベクトルの取り方は、
ベクトルの取り方は、![]() を基準にとる(下図)。 これで内積も計算できる。
を基準にとる(下図)。 これで内積も計算できる。
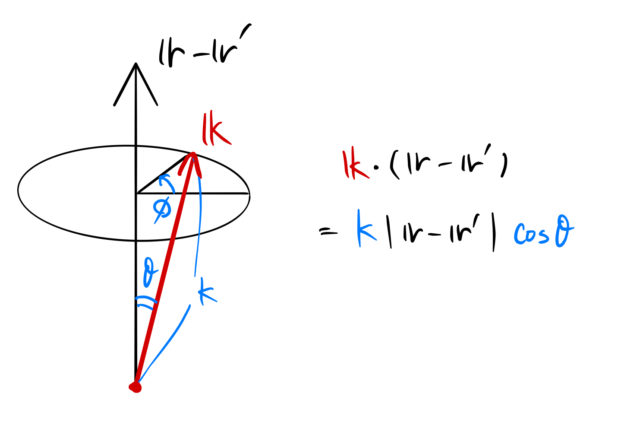
積分計算していこう。 ![]() は簡単に積分できる。
は簡単に積分できる。![]() の積分の後、
の積分の後、![]() の積分を実行する。
の積分を実行する。
![Rendered by QuickLaTeX.com \begin{eqnarray*} G({\bfr}-{\bfr}')&=& -\frac{1}{(2\pi)^3}\iiint\frac{e^{i{\bfk}\cdot({\bfr}-{\bfr}')}}{k^2}\,d{\bfk}\\\\ &=& -\frac{1}{(2\pi)^3}\int_{0}^{2\pi}d\phi \int_{0}^{\pi}d\theta\int_{0}^{\infty}dk \,\frac{e^{ik|{\bfr}-{\bfr}'|\cos\theta}}{k^2}\, k^2\sin \theta\\\\ &=& -\frac{1}{(2\pi)^3}\,2\pi\, \int_{0}^{\pi}d\theta\int_{0}^{\infty}dk \,e^{ik|{\bfr}-{\bfr}'|\cos\theta}\sin \theta\\\\ &=& -\frac{1}{4\pi^2} \int_{0}^{\infty}dk \left[-\frac{e^{ik|{\bfr}-{\bfr}'|\cos\theta}}{ik|{\bfr}-{\bfr}'|}\right]_0^{\pi}\\\\ &=& \textcolor{red}{-}\frac{1}{4\pi^2} \int_{0}^{\infty}dk \frac{e^{ik|{\bfr}-{\bfr}'|}-e^{-ik|{\bfr}-{\bfr}'|}} {ik|{\bfr}-{\bfr}'|}\\\\ &=&-\frac{1}{4\pi^2} \int_{0}^{\infty}dk \frac{2\sin k|{\bfr}-{\bfr}'|}{k|{\bfr}-{\bfr}'|}\quad(\because\sin \theta=\frac{e^{i\theta}-e^{-i\theta}}{2i})\\\\ &=&-\frac{1}{4\pi^2}\, \frac{2}{|{\bfr}-{\bfr}'|}\textcolor{red}{\int_{0}^{\infty} \frac{\sin x}{x}\,dx}\quad(x=k|{\bfr}'-{\bfr}'|)\\\\ &=&-\frac{1}{4\pi^2}\, \frac{2}{|{\bfr}-{\bfr}'|}\textcolor{red}{\frac{\pi}{2}}\\\\ &=&-\frac{1}{4\pi|{\bfr}-{\bfr}'|}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-e45cb1877a7a85696a88b344ed6bd422_l3.png)
最後の赤字の積分はディリクレ積分として知られており、 複素積分を用いて解くことができる。
以上、Green関数を求めることができた。 結果は重要である。
![]()
【結果】ポアソン方程式の解:スカラーポテンシャル
以上より、 スカラーポテンシャルが求めることができる。
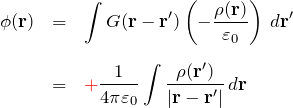
これは重要な結果である。 また、ここで扱ったGreen関数のおおまかなイメージは「Green関数の簡単な意味(基礎)」を参考にされたい。
3. よく見る具体的な形
最後に具体的な形をまとめおこう。
空間の電荷が電荷密度によって表されている場合:
![]()
原点に点電荷![]() がある場合:
がある場合:
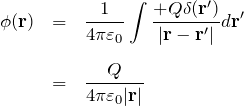
![]() に点電荷
に点電荷![]() がある場合:
がある場合:
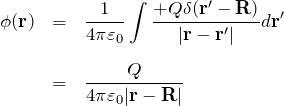
異なる位置に複数の点電荷![]() がある場合:
がある場合:
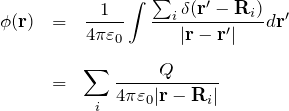
4. まとめ
偏微分方程式、フーリエ変換、極座標積分、ディリクレ積分、Green関数など計算は大変だったと感じる。ただ、得られた結果は重要なものである。 Green関数を使った微分方程式の解法としての練習問題にもよかろう。