確率漸化式でよくある問題として、正四面体の点の移動を図解する。例題は以下の通り。
例題
(1)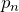 と
と 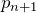 の漸化式を求めよ。
の漸化式を求めよ。
(2)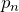 を求めよ。
を求めよ。
- 四面体ABCDの頂点を移動する点がある
- 1秒ごとに隣り合う頂点へ1/3の確率で移動する
- n秒後に点が頂点Aにいる確率を
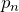 とする
とする - はじめ(0秒)のときには点は頂点A (
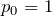 )
)
(1)
(2)
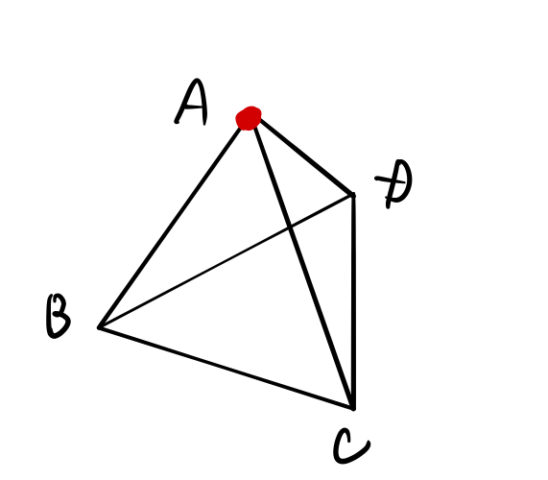
1. 状態は2つしかない!
今の例題の場合、何秒後でも状態は2つしかない。
- 点が頂点Aにいるか
- 点が頂点Aにいないか
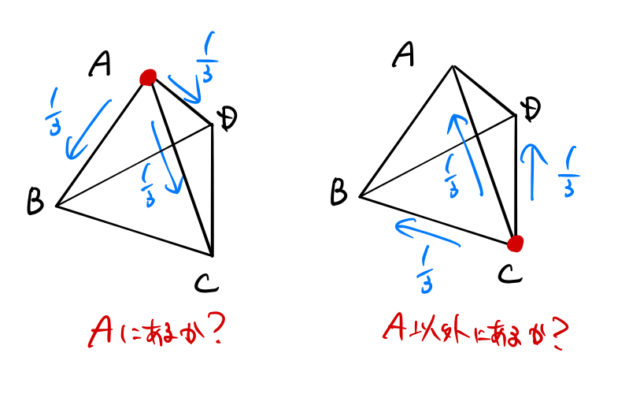
したがって、![]() 秒後の状態は、
秒後の状態は、
- 点が頂点Aにいる確率
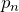
- 点が頂点Aにいない確率
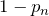
である。確率は足して1になっている。
2. 漸化式をつくる
![]() 秒後 と
秒後 と ![]() 秒後にどうなっているか?下のような図が描くのが良いでしょう。
秒後にどうなっているか?下のような図が描くのが良いでしょう。
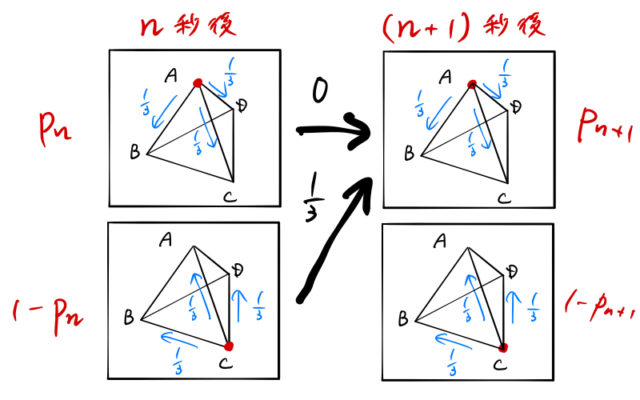
矢印の意味は下の通り。
- 0:
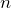 のときに 頂点A にいる場合は
のときに 頂点A にいる場合は 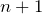 のときには B,C,D のいずれかに移る
のときには B,C,D のいずれかに移る - 1/3:
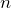 のときに 頂点A にいない場合は
のときに 頂点A にいない場合は 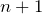 のときに A に 1/3 の確率で移る
のときに A に 1/3 の確率で移る
解答用紙に絵を描く場合は、下の簡略した絵で良い。
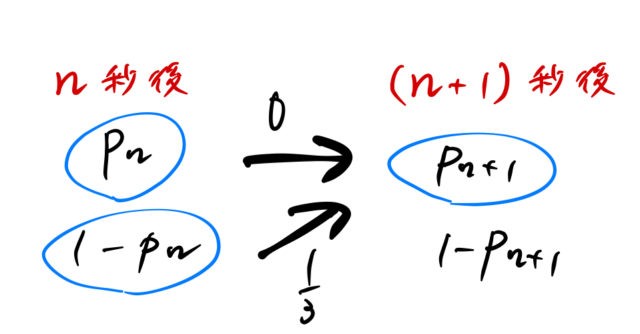
この絵から漸化式が作れる。
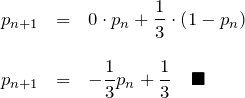
これが例題(1)の答えになる。
3. 漸化式を解く
漸化式の特性方程式を作る。![]() と
と ![]() を
を ![]() と置いた方程式を解く。
と置いた方程式を解く。
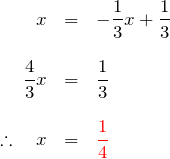
したがって、漸化式は下のように変形できる。このとき、展開して元に戻るかどうかをチェックする癖をつけると計算ミスが減る。
![]()
これは、数列 ![]() が公比 -1/3 の等比数列になっていることを表している。
が公比 -1/3 の等比数列になっていることを表している。![]() とおくと見やすくなるかもしれない。
とおくと見やすくなるかもしれない。
等比数列を解く:
公式を使わない方法で解く。これは ![]() の数字をどんどん減らしていけば良い。以下、色付きの部分に注目してほしい。
の数字をどんどん減らしていけば良い。以下、色付きの部分に注目してほしい。
![Rendered by QuickLaTeX.com \begin{eqnarray*} p_{n}-\frac{1}{4}&=& -\frac{1}{3}\textcolor{red}{\left(p_{n-1} -\frac{1}{4}\right)} \\ \\ &=& -\frac{1}{3}\, \textcolor{red}{\left[-\frac{1}{3}\left(p_{n-2} -\frac{1}{4}\right)\right]}\\ \\ &=& \left(-\frac{1}{3}\right)^2\, \textcolor{blue}{\left(p_{n-2} -\frac{1}{4}\right)} \\ \\ &=& \left(-\frac{1}{3}\right)^2\, \textcolor{blue}{\left[-\frac{1}{3}\left(p_{n-3} -\frac{1}{4}\right)\right]} \\ \\ &=&\cdots \\ \\ &=& \left(-\frac{1}{3}\right)^n\, \left(p_0 -\frac{1}{4}\right) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-e9fc44414e01e8791ccc8f454d4e7d90_l3.png)
● ![]() か
か ![]() か迷う方は下の図のように求めればよい(等比数列の一般項を求めるコツ)。
か迷う方は下の図のように求めればよい(等比数列の一般項を求めるコツ)。
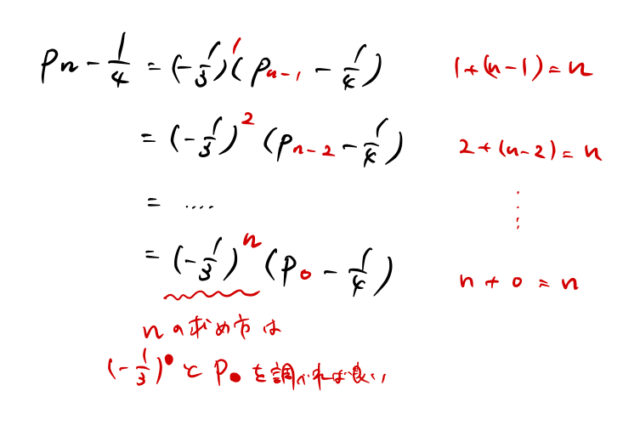
![]() を求める:
を求める:
初期状態(0秒の時)は点は頂点 A にいるため、![]() である。
である。
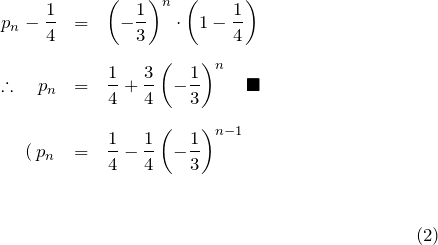
![]() が求められたら
が求められたら ![]() を確認すると計算ミスが防げる。ここで
を確認すると計算ミスが防げる。ここで ![]() の意味は、はじめAにいる状態から1秒後にはB,C,Dのいずれかに点が移動するために確率が0になっているということである。
の意味は、はじめAにいる状態から1秒後にはB,C,Dのいずれかに点が移動するために確率が0になっているということである。
4. まとめ
絵を描いて確率漸化式を細かく見てきた。
- 漸化式の作り方(絵の描き方)
- 計算ミスを防ぐコツ
- 特性方程式を用いた漸化式の変形
- 等比数列の解き方
これらが理解できれば、確率漸化式のどの問題でも対応できる(大学入試レベル)。