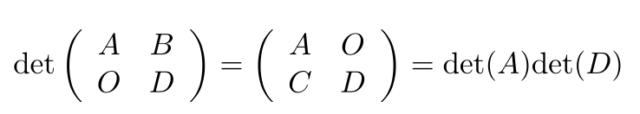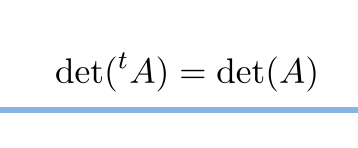行列式が下のような対称な形の場合に重要な関係がある。以下を示す。
重要な行列式の公式
![]() は
は ![]() 次正方行列のときに以下が成り立つ。
次正方行列のときに以下が成り立つ。
![]()
1. det(A B O C) = det(A)det(C)
下の関係式を使う。零行列があるときは簡単に行列式が計算できる。
零行列  があるときの行列式
があるときの行列式
![]()
※この証明は見かけ以上に面倒である。![]() がそれぞれ 2
がそれぞれ 2![]() 2 なら簡単に証明できるのが、一般の
2 なら簡単に証明できるのが、一般の ![]() 次正方行列の場合はちょっと大変。
次正方行列の場合はちょっと大変。
上の形を作れば簡単に行列式が計算できる。
2. 証明
証明:零行列ができるように式変形していく。行列は ![]() であることに注意する。
であることに注意する。
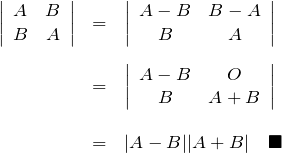
- 1つ目の等号:(
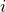 行目)-(
行目)-(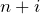 行目)(
行目)(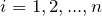 )
) - 2つ目の等号:(
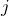 列目)+(
列目)+(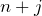 行目)(
行目)(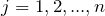 )
) - 3つ目の等号:「項目1」の関係を使う
![]() 次行列を
次行列を ![]() 次行列のブロックに分けて行列式の変形するのがコツ。
次行列のブロックに分けて行列式の変形するのがコツ。
3. まとめ
証明自体は零行列を作るように行列式を変形していくだけなので難しくはないでしょう。行列式をブロックに分けるのはよく使う手法です。
![]() 行列式の計算が出題されたりした場合に、上の関係が使えるかどうか考えるのがいいでしょう。
行列式の計算が出題されたりした場合に、上の関係が使えるかどうか考えるのがいいでしょう。