![]() を
を ![]() で表すための計算をおこなう。これは、2階微分を含んだラプラシアンの極座標表示を導くときに使う。よくみる結果だけ最初に示す。
で表すための計算をおこなう。これは、2階微分を含んだラプラシアンの極座標表示を導くときに使う。よくみる結果だけ最初に示す。
1階微分の極座標表示
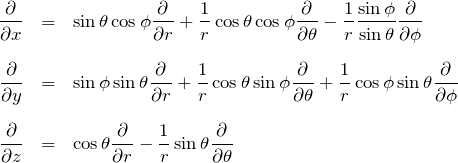
目次
1. 極座標表示
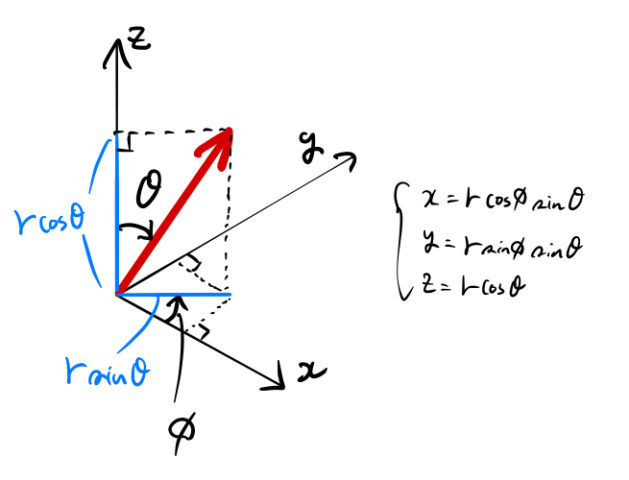
一般的な極座標変換は以下の図に従えば良い。![]() と
と ![]() の取り方に注意してほしい。
の取り方に注意してほしい。
変換 ![]() は以下の通りである。
は以下の通りである。
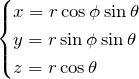
2. 1階の偏微分を極座標表示
目標:![]() を
を ![]() で表す。
で表す。
微分のチェーンルールより、
![]()
である。![]() に関しても同様である。
に関しても同様である。
2.1 ∂r/∂x、∂r/∂y、∂r/∂z
![]() について:
について:
極座標変換から、
![]()
である。これの両辺を ![]() で偏微分して、
で偏微分して、
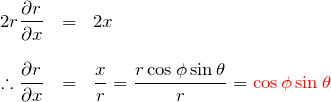
![]() についても同様に、
についても同様に、
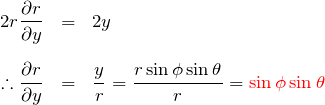
である。![]() について、
について、
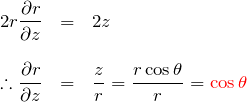
となる。
2.2 ∂θ/∂x、∂θ/∂y、∂θ/∂z
![]()
より
![]()
である。両辺を ![]() で偏微分して、
で偏微分して、
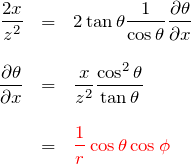
![]() についても同様に、
についても同様に、
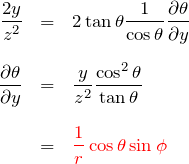
![]() については、
については、![]() をとったものを微分して計算する。
をとったものを微分して計算する。
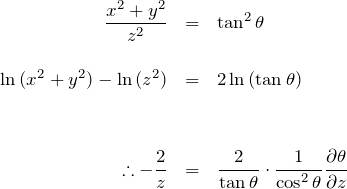
である。したがって、
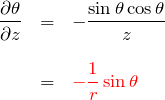
2.3 ∂φ/∂x、∂φ/∂y、∂φ/∂z
![]()
を利用する。両辺を ![]() で偏微分して、
で偏微分して、
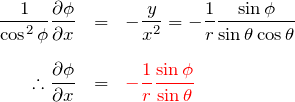
![]() について、
について、
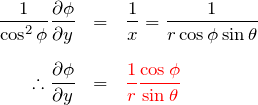
![]() について、
について、![]() は
は ![]() に依存しない(
に依存しない(![]() は
は ![]() 平面内の角度)。したがって、
平面内の角度)。したがって、
![]()
2.4 ∂/∂x、∂/∂y、∂/∂z を極座標表示
上の結果をすべてまとめる。![]() についてチェーンルール(*) より、
についてチェーンルール(*) より、
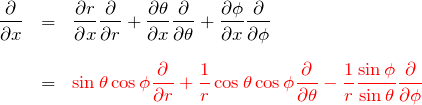
![]() について:
について:
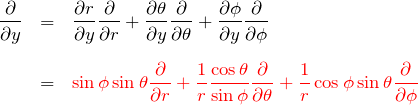
![]() について:
について:
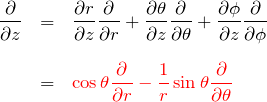
以上で、1階微分を極座標表示できた。再度まとめておく。
1階微分の極座標表示
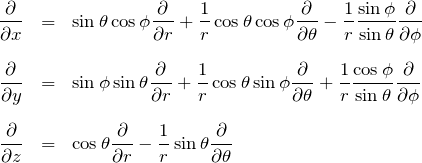
3. まとめ
計算のポイントは、
- チェーンルールを使う
- うまい変形を使う(計算量を減らす)
- 1個1個丁寧に求める
ことである。
一度導出したら2度とやりたくない計算ではある。しかし、鬼畜の所業はラプラシアンの極座標表示に続く。