ここではデータ点を 一次関数 を用いて最小二乗法でフィッティングする。二次関数・三次関数でのフィッティング式は こちら 。
下の5つのデータを直線でフィッティングする。
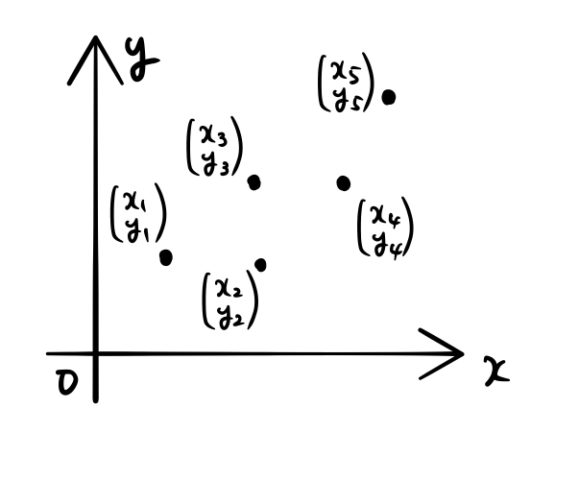
1. 最小二乗法とは?
フィッティングの意味
フィッティングする一次関数は、
![]()
の形である。データ点をフッティングする直線を求めたいということは、知りたいのは傾き ![]() と切片
と切片 ![]() である!
である!
上の5点のデータに対して、下のようにいろいろ直線を引いてみよう。それぞれの直線に対して 傾きと切片 が違うことが確認できる。
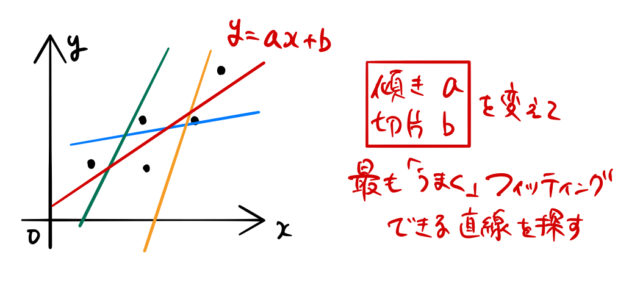
こうやって、自分で傾きと切片を変化させていき、最も「うまく」フィッティングできる直線を探すのである。
「うまい」フィッティング
「うまく」フィッティングするというのは曖昧すぎる。だから、「うまい」フィッティングの基準を決める。
試しに引いた赤い直線と元のデータとの「差」を調べる。たとえば ![]() 番目のデータ
番目のデータ ![]() に対して、直線上の点
に対して、直線上の点 ![]() とデータ点
とデータ点 ![]() との差を見る。
との差を見る。
![]()
しかしこれは、データ点が直線より下側にあればマイナスになる。単にどれだけズレているかを調べるためには、二乗してやれば良い。
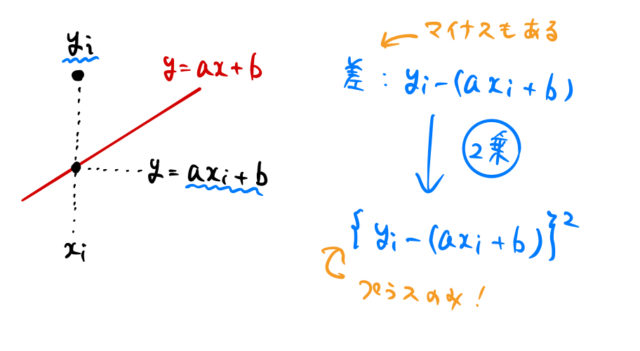
これでズレを表す量がプラスの値になった。他の点にも同じようなズレがあるため、それらを全部足し合わせてやればよい。どれだけズレているかを総和したものを ![]() とおいておく。
とおいておく。
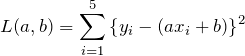
この関数は ![]() を2変数とする。これは、傾きと切片を変えることは、直線を変えるということに対応し、直線が変わればデータ点からのズレも変わってくることを意味している。
を2変数とする。これは、傾きと切片を変えることは、直線を変えるということに対応し、直線が変わればデータ点からのズレも変わってくることを意味している。
最小二乗法
あとはデータ点からのズレの最も小さい「うまい」フィッティングを探す。これは、2乗のズレの総和 ![]() を最小にしてやればよい。これが最小二乗法だ!
を最小にしてやればよい。これが最小二乗法だ!
![]() は2変数関数であった。したがって、下図のように
は2変数関数であった。したがって、下図のように ![]() が最小となる点を探して、
が最小となる点を探して、![]() (傾き、切片)を求めれば良い
(傾き、切片)を求めれば良い![]() 。
。
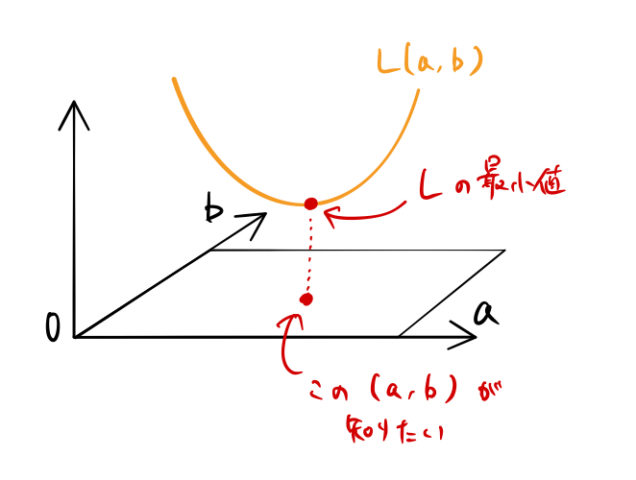
2変数関数の最小値を求めるのは偏微分の問題である。以下では具体的に数式で計算する。
2. 最小値を探す
最小値をとるときの条件
![]() の2変数関数の最小値になる
の2変数関数の最小値になる ![]() は以下の条件を満たす。
は以下の条件を満たす。
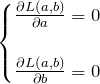
2変数に慣れていない場合は、![]() を思い出してほしい。下に凸の放物線の場合は、
を思い出してほしい。下に凸の放物線の場合は、![]() のときの
のときの ![]() で最小値になるだろう(接線の傾きゼロ)。
で最小値になるだろう(接線の傾きゼロ)。
計算
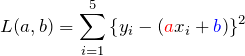
を ![]() で偏微分する。中身の微分とかに注意する。
で偏微分する。中身の微分とかに注意する。
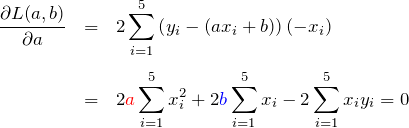
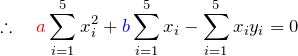
![]() で偏微分
で偏微分
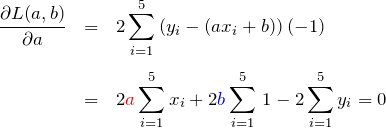
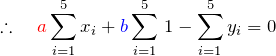
上の2つの式は ![]() に関する連立方程式である。行列で表示すると、
に関する連立方程式である。行列で表示すると、
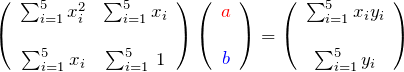
逆行列を作って、
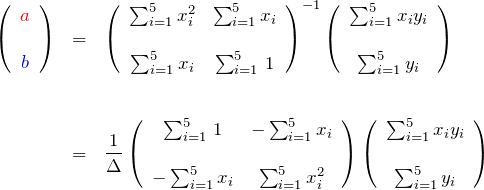
ここで、
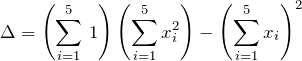
である。したがって、最小二乗法で得られる傾き ![]() と切片
と切片 ![]() がわかる。データ数を
がわかる。データ数を ![]() として一般化してまとめておく。
として一般化してまとめておく。
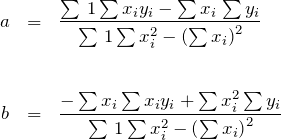
ただし、
式が煩雑に見えるが、用意されたデータをかけたり、足したり、2乗したりして足し合わせるだけなので難しくないでしょう。
式変形して平均値・分散で表現
![]()
はデータ数 ![]() を表す。
を表す。
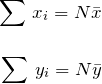
はそれぞれ、![]() の総和と
の総和と![]() の総和なので、平均値とデータ数で表すことができる。
の総和なので、平均値とデータ数で表すことができる。
![]()
は同じく ![]() の総和であり、2乗の平均とデータ数で表すことができる。
の総和であり、2乗の平均とデータ数で表すことができる。
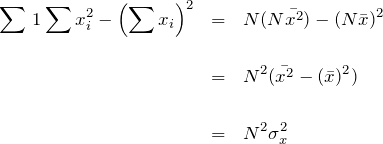
![]() の分母の項は
の分母の項は ![]() の分散の2乗によって表すことができる。
の分散の2乗によって表すことができる。
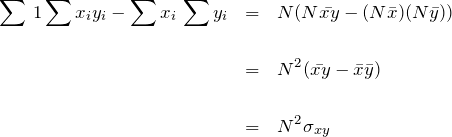
は共分散として表すことができる。
最後に ![]() の分子は、
の分子は、
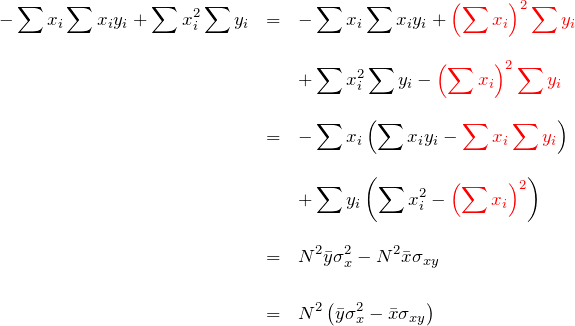
赤色の項は分散と共分散で表すために挟み込んだ。
以上より一次関数 ![]() は、
は、
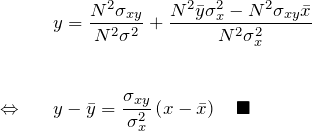
よく見かける式と同じになる。
3. まとめ
最小二乗法が何をやっているかわかれば、二次関数など高次の関数でのフィッティングにも応用できる。
![]() :下に凸になるのは
:下に凸になるのは ![]() の形を見ればわかる。
の形を見ればわかる。