リカッチ(リカティ、Riccati)の微分方程式は
![]()
の形をしている。一般的には解けないが、 1つの特解 ![]() がわかっているときは
がわかっているときは ![]() とおくことでベルヌーイの微分方程式に帰着して解ける。ベルヌーイ型は線形型に帰着するため
とおくことでベルヌーイの微分方程式に帰着して解ける。ベルヌーイ型は線形型に帰着するため
リカッチ型 → ベルヌーイ型 → 線形型
のようにより簡単な微分方程式に帰着させて解く。 ここでは例題を通して、リカッチ型の解法を習得しよう。
以下のリカッチの微分方程式の特解を見つけて解こう。
![]()
目次
1. リカッチの微分方程式の解き方
特殊なタイプの微分方程式は、「解けるタイプの微分方程式」に帰着させて解く。リカッチ型はベルヌーイ型に帰着される。
ベルヌーイの微分方程式とは?
もしベルヌーイ型の微分方程式の形とその解法がわからなければ、先にそちらを習得するべきである。ここでは簡単に、ベルヌーイ型の微分方程式をまとめておく。
ベルヌーイ型:
![]()
で
線形型:
![]()
ベルヌーイ型に帰着することを確認
リカッチの微分方程式
![]()
の特解の一つを ![]() とする。つまり、
とする。つまり、
![]()
である。
リカッチ型の解の形を ![]() と置く。
と置く。
![]() より微分方程式は、
より微分方程式は、
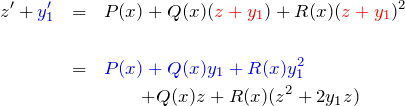
(*)より、青色の部分は消えるため、
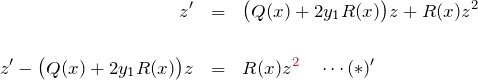
となる。これは、![]() に関するベルヌーイ型の微分方程式である。
確かにリカッチ型はベルヌーイ型に帰着する。
に関するベルヌーイ型の微分方程式である。
確かにリカッチ型はベルヌーイ型に帰着する。
リカッチの微分方程式の一般解
上のベルヌーイ型を解く。
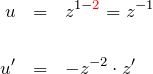
より、ベルヌーイ型(*)’の両辺に ![]() をかける。
をかける。
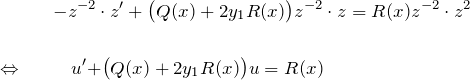
となり、線形型に帰着する。
したがって、両辺に
![]()
をかけて、
![]()
![]()
以上より、
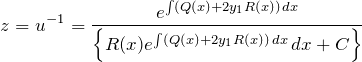
したがって、リカッチ型の一般解は
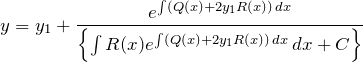
である。当たり前だが、これは覚える式ではない。
解き方の流れまとめ
リカッチ型を解くための前提は
- 特解が見つけられる
- ベルヌーイ型が解ける
- 線形型が解ける(ベルヌーイ型は線形型に帰着するため)
リカッチの微分方程式
![]()
- 特解
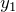 を見つける
を見つける - 解を
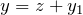 とおくと
とおくと  に関してベルヌーイの微分方程式になる
に関してベルヌーイの微分方程式になる 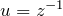 とおいて線形型に帰着させる(ベルヌーイの微分方程式の解法)
とおいて線形型に帰着させる(ベルヌーイの微分方程式の解法) - 線形型を解いて
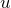 を求める(1次線形型微分方程式の解法)
を求める(1次線形型微分方程式の解法) 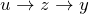 と変数を戻す
と変数を戻す
2. 例題の解答
以下の解答で、![]() は定数である。 (1)は変数分離型でも解ける。
は定数である。 (1)は変数分離型でも解ける。
例題(1)の解答
特解を探す:
![]()
の特解の一つは
![]()
である。
![]() と置く:
と置く:
![]()
より
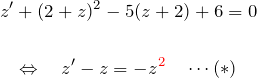
のベルヌーイ型(あるいは変数分離型)。 ここでは練習のため、ベルヌーイ型として解く。
![]() と置く:
と置く:
![]()
より、(*)の両辺に ![]() をかけて
をかけて
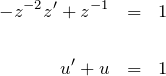
の線形型(あるいは変数分離型)になる。
両辺にかけるもの:
![]()
両辺に ![]() をかける:
をかける:
![Rendered by QuickLaTeX.com \begin{eqnarray*} &&e^{x} u'+e^{x} u=e^{x}\\\\ \Leftrightarrow \quad&& \frac{d}{dx}\left[e^{x} u\right]= e^{x}\\\\ \Leftrightarrow \quad&& e^{x}u=\int e^{x}\,dx=e^{x}+C\\\\ \Leftrightarrow \quad&& u=1+Ce^{-x} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-0118ac169e6ce2f43ba8fde68fbf6945_l3.png)
![]() :
:
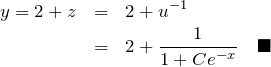
*答え方は定数項 ![]() の取り方で変わる。
以下のような形でもよい。
の取り方で変わる。
以下のような形でもよい。
![]()
例題(2)の解答
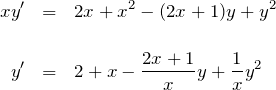
はリカッチ型で、特解の一つは ![]() である。
つまり、
である。
つまり、
![]()
が成り立つ。
![]() と置く:
と置く:
![]()
より
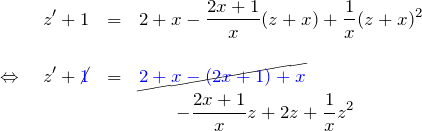
したがって、
![]()
のベルヌーイ型に帰着する。
![]() と置く:
と置く:
![]()
より、ベルヌーイ型の両辺に ![]() をかけて
をかけて
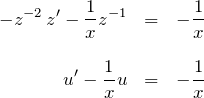
の線形型に帰着する。
両辺にかけるもの:
![]()
線形型の両辺に ![]() をかける:
をかける:
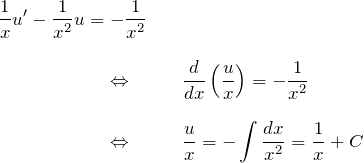
したがって
![]()
![]() :
:
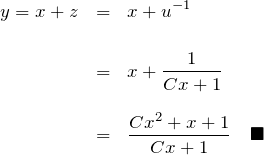
3. まとめ
リカッチの微分方程式の解き方を学んだ。特解を見つけてから
リカッチ型 → ベルヌーイ型 → 線形型
と帰着させることで解けることがわかった。 ポイントである、![]() の置き方だけ覚えておけば良いだろう。
の置き方だけ覚えておけば良いだろう。