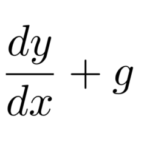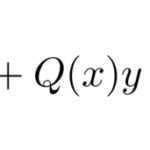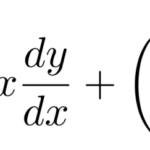微分方程式とは何か→微分の入った方程式である
解散!
とするとWikipediaの最初の1文レベルなので、 ちゃんと微分方程式とは何かを説明していく。また、どのような形になっているかを説明して、 簡単な例題を実際に解いてみることにする。
目次
1. 物理に現れる微分方程式
微分方程式とは何か?
まず、微分入りの方程式を微分方程式と呼ぶ。
いくつか例を挙げておこう。微分の書き方も色々ある。
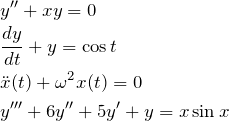
![]() は
は![]() の時間での1階微分、2階微分を表す。 物理では時間に対して物体の位置を追うため、この書き方が使われることもある。
の時間での1階微分、2階微分を表す。 物理では時間に対して物体の位置を追うため、この書き方が使われることもある。
高校物理ではじめに登場する微分方程式
高校物理で微分を使うことはタブーとされているが、 最初に出会う微分方程式はおそらく以下の運動方程式であろう。
![]()
この書き方だと、どこに微分が使われているかが分かりにくい。 加速度 ![]() が速度
が速度 ![]() の時間微分であり、 速度
の時間微分であり、 速度 ![]() もまた位置
もまた位置 ![]() の時間微分であることを思い出す。 (時間の微分についての簡単な注釈を最後につけた
の時間微分であることを思い出す。 (時間の微分についての簡単な注釈を最後につけた![]() )
)
こういうわけで運動方程式は
![]()
となり、微分が入った方程式になる。 ここでは2階微分が入っているため、「2階微分方程式」と呼ぶ。 「微分方程式を解く」とは、上の方程式を満たす ![]() を探すことである。
を探すことである。
*時間微分の簡単な説明:10秒のうちに100m進めば平均して1秒間に10m進む。 ということは、0.1秒あたり平均して1m進むし、0.01秒あたり0.1m進む。 つまり、![]() 秒あたり 10/
秒あたり 10/![]() m だけ平均して進む。 この時間の間隔をどんどん小さくしていけば(
m だけ平均して進む。 この時間の間隔をどんどん小さくしていけば(![]() )、「平均の速度」は「ある瞬間の速度」になる。
)、「平均の速度」は「ある瞬間の速度」になる。 ![]() を進んだ距離として
を進んだ距離として ![]() は速度を表す。
は速度を表す。
簡単な微分方程式を解いてみる
右辺の力 ![]() が物体に働く重力
が物体に働く重力 ![]() として(上向きをプラス)、 これを解いていこう。
として(上向きをプラス)、 これを解いていこう。
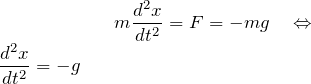
ここでの考え方は、
「微分された結果、右辺の ![]() (定数)となっている」
(定数)となっている」
ため
「両辺を時間で積分していけば良い」
ということである。
積分(1回目):
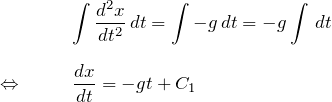
左辺は2階微分されたものを積分するので、1階微分になる。 右辺は定数なので積分の外に出す。両辺とも不定積分なので積分定数がでてくるが、 全部右辺の ![]() にまとめた。
にまとめた。
積分(2回目):
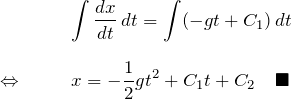
左辺は1階微分だったので、積分して元に戻る。 右辺は ![]() の1次と定数の積分なので、結果は
の1次と定数の積分なので、結果は ![]() の2次と1次になる。 積分定数は全部
の2次と1次になる。 積分定数は全部 ![]() にまとめた。
にまとめた。
これが答えだ。
この微分方程式の解は、高校物理において「自由落下の位置を表す公式」として与えられる。
![]()
ここで、積分定数は ![]() 、
、![]() のように初期値に置き換えた。 不定積分とは積分区間の決まっていない積分のことであり、それは物理では初期値の決まっていないことを表す。
のように初期値に置き換えた。 不定積分とは積分区間の決まっていない積分のことであり、それは物理では初期値の決まっていないことを表す。
これが微分方程式の解き方である。複雑でなければ基本的には積分していけば答えにたどりつく。 最も簡単な微分方程式は以上である。
2. 微分方程式の難しさ
おっと、上では積分していけば答えがわかると書いた。しかし、それほど単純でもない。
積分だけでは解けない
下の問題を見てほしい。
![]()
この ![]() を求めたい。
を求めたい。
上のように、積分してみよう。
![]()
見てわかる通り、![]() が求められていない。 微分方程式が積分方程式に変わっただけである。
が求められていない。 微分方程式が積分方程式に変わっただけである。
したがって、一般的に微分方程式を解くためには 「何か別の方法」が必要である。
よくある解き方の一つは、解の形を決めてしまうことである。 ![]() のように決めておく(
のように決めておく(![]() は
は ![]() でない定数)。 そうすれば、
でない定数)。 そうすれば、
![]() を求める問題→
を求める問題→ ![]() を求める問題
を求める問題
に変わった。
この ![]() を元の微分方程式に代入して、
を元の微分方程式に代入して、
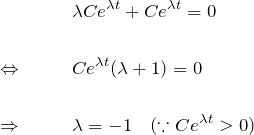
のように ![]() を求めることができた。 したがって答えは
を求めることができた。 したがって答えは
![]()
となる。このように解の形を決めてしまうことで解ける微分方程式もある。
微分方程式を解くための勉強法
上で紹介してきた2つの微分方程式は、数多の微分方程式の中で最も簡単なものである。 微分方程式のタイプによって解き方がたくさんある。
これから微分方程式を解いていこうという方は、 「このタイプの微分方程式ならこういう解法」 というパターンを習得していかなくてはならない。
そういうわけで、微分方程式を解くためには暗記が少なからず必要になってくるだろう。
あと、色々な関数の微分・積分がちゃんとできないと、そもそも微分方程式を解くことができない。雪山に半袖で行くようなものである。
3. まとめ
微分方程式とは何かを説明して、簡単な微分方程式を解いてきた。 これから微分方程式を一生懸命解かれるという方は、 さまざまなタイプの微分方程式に出会うことになる。
ただし、微分方程式は解き方わかればイージモードである。