数学検定1級(数検1級)によくでる三乗根を簡単に計算する方法を紹介します。数検1級に受かる上では知っておくべき計算のひとつでしょう。ここでは、2乗根の二重根号の例をはじめに計算して、三乗根へとつなげます。
今回、解きたいのは以下の数検1級1次レベルである以下の問題だ。
次の根号を簡単にせよ。
![]()
1. 二重根号を簡単に(高校数学)
これは高校レベルでしょうか。順番に見ていきます。とりあえず例題。
次の根号を外せ。
![]()
簡単に外せそうです。
【解答】
![]()
絶対値を忘れ無いでください。なぜ絶対値がつくかわから無い方は、![]() 、
、![]() で計算すると分かると思う。左辺のルートは正です。結局、ルートの中に2乗を作ればいいだけです。
で計算すると分かると思う。左辺のルートは正です。結局、ルートの中に2乗を作ればいいだけです。
次の例題へ行きましょう。
1.1 よく出る2重根号を外す問題
次の根号を外して簡単にせよ。
![]()
二重根号の問題で、高校数学レベルです。解き方は、![]() の形にすれば良いのでした。つまり、
の形にすれば良いのでした。つまり、![]() の形を目指す。(問題として出されている以上
の形を目指す。(問題として出されている以上 ![]() の中身が
の中身が ![]() となるはずです。)
となるはずです。)
【解答】
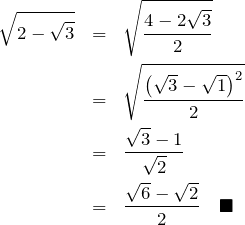
最後の有理化はしなくても正解です。途中の ![]() のところで、
のところで、![]() としても構いませんが、絶対値を気にし無いといけないので避けた方がいいでしょう。「√(大きい数)-√(小さい数) 」が無難である。
としても構いませんが、絶対値を気にし無いといけないので避けた方がいいでしょう。「√(大きい数)-√(小さい数) 」が無難である。
1.2 別解を考える
無理やり簡単にした形を仮定して解いてみるやり方を紹介します。先ほどの例で解説します。
次の根号を外して簡単にせよ。
![]()
ルートの中に ![]() が見えるので、簡単にした形にも
が見えるので、簡単にした形にも ![]() がありそうです。ということで
がありそうです。ということで ![]() を実数として下のように置く。
を実数として下のように置く。
![]()
両辺を2乗して整理する。
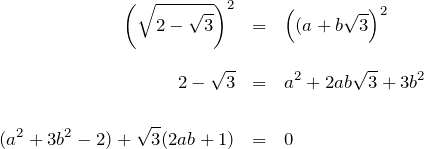
ここで、![]() は 実数であり
は 実数であり ![]() は無理数であるから、第1項は実数、第2項は無理数である。つまり、それぞれのカッコは0になる。
は無理数であるから、第1項は実数、第2項は無理数である。つまり、それぞれのカッコは0になる。
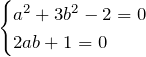
とにかく、この連立方程式を解いて ![]() を求めれば良い。この場合、下の式を2倍して上の式に足すと簡単に解ける。
を求めれば良い。この場合、下の式を2倍して上の式に足すと簡単に解ける。
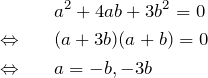
これを下の式に代入して ![]() が求められる。
が求められる。
![]()
1個目の方は、1.1の解法の答えと一致していることがすぐにわかる。2個目の ![]() について、
について、
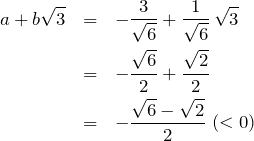
これは負になる。というのも、![]() と置いて2乗しているために解として、±の形で出てきてしまった。この場合は、
と置いて2乗しているために解として、±の形で出てきてしまった。この場合は、![]() であることから、プラスの解を答えとして取れば良い。もちろん、1.1の解き方と同じ結果になる。
であることから、プラスの解を答えとして取れば良い。もちろん、1.1の解き方と同じ結果になる。
![]()
これが高校数学のレベルである。
2. 3乗根を簡単に。
![]() 型の問題に移りたい。
型の問題に移りたい。
2.1 「つまらない」問題
次の3重根を簡単にせよ。
![]()
簡単に解ける。
![]()
絶対値はいらない。![]() のように3乗根はルートの中に負の数が入る時もある。
のように3乗根はルートの中に負の数が入る時もある。
2.2 「つまる」問題(数検1級レベル)
![]() として
として ![]() を展開したもので問題を作る。
を展開したもので問題を作る。
![]()
である。![]() を答えにして問題を作ると下のようになる。
を答えにして問題を作ると下のようになる。
次の根号を簡単にせよ。
![]()
急に難しく見えるだろう。2乗根のときと同じ1.1 の方法で、![]() の中身を
の中身を![]() の形に持っていくのは難しい。これは式の展開は簡単に行えるが、因数分解は難しいということを意味している。大きな素数同士の積を素因数分解するのが難しいというRSA暗号と同じような理屈であろう。
の形に持っていくのは難しい。これは式の展開は簡単に行えるが、因数分解は難しいということを意味している。大きな素数同士の積を素因数分解するのが難しいというRSA暗号と同じような理屈であろう。
そこで、1.2 の方法を継承することになる。![]() の
の![]() に注目して、根号を外した形を仮定する。
に注目して、根号を外した形を仮定する。![]() は実数とする。
は実数とする。
![]()
両辺を3乗して整理する。
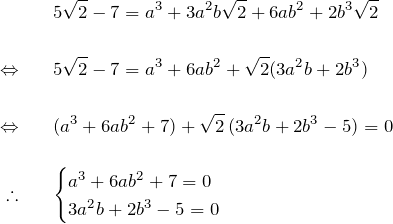
この連立方程式を解いて ![]() を求めれば良い。ただし、この連立方程式は解きにくいため、上式を5倍、下式を7倍して足して定数項を消してみる。そうすると新しい式を得る。
を求めれば良い。ただし、この連立方程式は解きにくいため、上式を5倍、下式を7倍して足して定数項を消してみる。そうすると新しい式を得る。
![]()
これは、以下の ![]() の因数を求める問題と同じ要領で求められる。
の因数を求める問題と同じ要領で求められる。
![]() の因数を求めよ。
の因数を求めよ。
![]()
数検の1次の問題で出題されるのであれば、係数はそこまで複雑ではない(だろう)。そして、もっと綺麗に連立方程式が解けるように作られてるとも思う。
ここでは、容易に ![]() がわかるので因数定理より
がわかるので因数定理より ![]() を因数にもつ。以下の因数分解は、解の公式やらを用いて複素数の範囲でおこなった
を因数にもつ。以下の因数分解は、解の公式やらを用いて複素数の範囲でおこなった
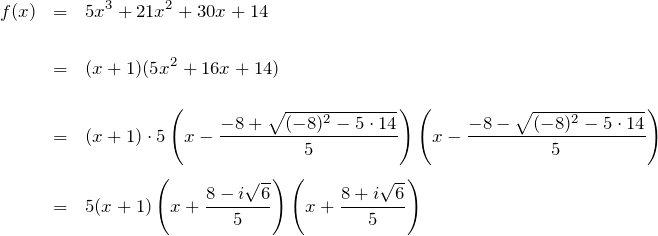
もちろん実係数 ![]() を考えているため、
を考えているため、![]() をとる。このときの
をとる。このときの ![]() は、
は、
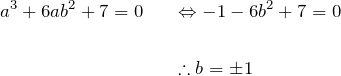
となる。したがって、![]() となる。ここで以下の式に戻って、
となる。ここで以下の式に戻って、
![]()
の ![]() は正であるため、左辺の
は正であるため、左辺の ![]() である。
である。
一方で、![]() のとき右辺が負になるので不適。
のとき右辺が負になるので不適。![]() のときは、
のときは、![]() より適。したがって、
より適。したがって、
![]()
と簡単にすることができる。 ![]()
3重根を外す問題のポイントは以下の通り。
![]()
ここで、![]() 型については考えなかった。これは、根号の中身の
型については考えなかった。これは、根号の中身の ![]() が互いに素の場合などに、展開したものが綺麗にまとまらないことがあるためである。言ってしまえば複雑になり面倒なのである。
が互いに素の場合などに、展開したものが綺麗にまとまらないことがあるためである。言ってしまえば複雑になり面倒なのである。
3. まとめ
二重根号の外し方を扱いました。3乗根のパターン数検1級の1次試験で出るような問題です(計算が多い)。過去問に載ってたりしますが、受験者の方は習得しておくとよいでしょう。
あと「つまる」=「not つまらない」ではない。