全記事一覧 > 物理 > 固体物性

Wannier励起子とFrenkel励起子

　励起子（エキシトン；Exciton）は大きく分けてWannier励起子（ワニエ型）とFrenkel励起子（フレンケル型）の２種類ある。Wannier励起子は固体物理（特に無機物の半導体）において重要な励起状態である。一方で、Frenkel励起子は分子結晶において重要な励起子である。ここでは、この２つの励起子の違いの概要をまとめる。

　初学者を対象とした基本的な内容になっているために、詳細は書籍等に譲ることとする。


1. Wannier励起子

　光などが半導体に入射して価電子帯の電子（-)が励起されると、価電子帯には正孔が生成し、伝導帯には電子が生成する。このときに、電子と正孔の電荷は互いに逆符号であるためにクーロン力で結合し、互いに束縛された状態をとる（励起子状態）。

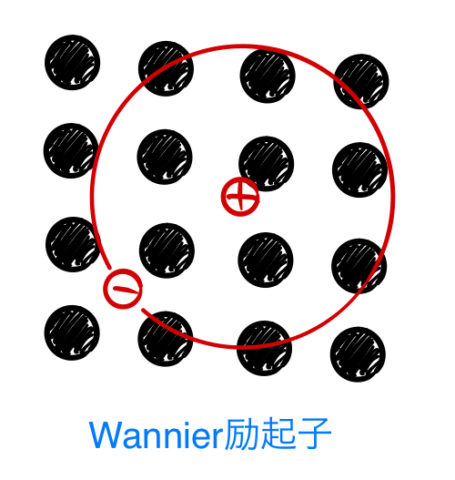
　図に半導体の場合の励起子状態を示した。半導体の場合、この励起子は結晶中に広がっていてWannier励起子と呼ばれる。Wannier励起子の励起子半径は後に説明するFrenkel励起子より大きい。以下に一般的なWannier励起子の性質をまとめた。

  • 無機物半導体でよく見られる
  • 励起子の典型的な半径は 10-100\, \text{\AA}
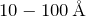
  • 励起子束縛エネルギーは水素原子モデルと同じように見積れる

1.1 励起子エネルギーと励起子半径

　正符号の電荷をもつ正孔と負符号の電荷をもつ電子のクーロン力による束縛状態は、水素原子のモデルと同じように計算することができる。よく知られているように、遠心力とクーロン力の釣り合いを考えれば良い。

    \begin{eqnarray*} E_{\rm exciton}&=&\frac{e^4}{2(4\pi\varepsilon_0)^2 \hbar^2}\frac{1}{\varepsilon_r^2}\frac{m_r}{m_0}\frac{1}{n^2} \quad {\rm [eV]}\\ &=& \frac{1}{\varepsilon_r^2}\frac{m^{*}_r}{m_0}\frac{1}{n^2} \quad {\rm [Ry]}\\ \\ a&=&\frac{4\pi \hbar^2 \varepsilon_0 \varepsilon_r}{m_r e^2} \quad {\rm [m]}\\ &=& \varepsilon \frac{m_0}{m_r^{*}} \quad {\rm [a_{B}]} \end{eqnarray*}

　ここで、エネルギーの単位についてリドベルグ単位、半径の長さの単位について原子単位(a.u.) を用いた。それぞれの単位系の変換は以下の通り。

  • 1 \,{\rm Ry} = 13.6 \,{\rm eV}
  • a_{\rm B}=0.529 \, \text{\AA}

　励起子エネルギーと励起子半径について、水素原子モデルとの違いは、比誘電率 \varepsilon_r と 有効質量 m_r^{*} である。単純に水素原子モデルにおけるエネルギーとボーア半径の式に対して、

  • \varepsilon_0 \rightarrow \varepsilon\equiv\varepsilon_0 \varepsilon_r
  • m_0 \rightarrow m_r^{*}

と置き換えれば励起子のエネルギーと半径が得られる。


1.2 光吸収（光学特性）

　励起子の存在により、光吸収は実際の直接バンドギャップ（E_g）に比べて小さいエネルギー帯で起こる。励起子のエネルギーは主量子数 n で区別され離散的な値をとる。

　また、E_{\rm exciton} はバンドギャップ E_g からどれだけエネルギーが小さいかを表す。したがって光吸収は E_g -E_{\rm exctiton} に対応するエネルギーでおこる。

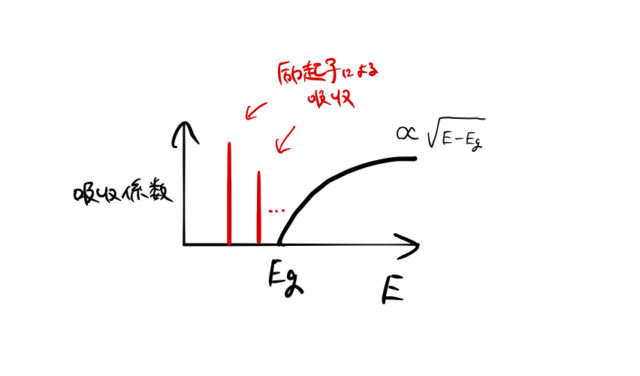
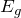吸収係数のエネルギー依存性。直接バンドギャップ E_g をもつ材料に対して、吸収係数はエネルギーの1/2乗に比例する。赤いピークは励起子の吸収に対応する。

　エネルギーの小さいところから主量子数 n の励起子に対応する。主量子数の小さいn=1 に対応する励起子の方が状態として安定であるために、吸収のピークは n=1 で基本的には大きくなる。

　ふつう、理論計算を行う場合に予想されるバンドギャップは励起子を含まないバンドギャップである。計算結果が実験と一致しない場合は、実験のバンドギャップエネルギーが励起子のエネルギーを測定している可能性もあることに注意する。計算で励起子を含んだ計算をするためには、例えば、ベーテ・サルピーター方程式(Bethe-Salpeter equaction)を解くなどする必要がある。

2. Frenkel励起子

　Frenkel励起子の半径はWannier励起子より小さい。より局在した励起子を考える。このような局在した励起子は分子結晶で起こりうる。局在性は分子軌道の波動関数が局在していることによる。典型的なFrenkel励起子の特徴は以下の通りである。

  • 分子結晶でよく見られる
  • 励起子の典型的な半径は 1-10\, \text{\AA}
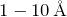
  • 分極波と関係する

　分子結晶の場合は、個体のバンドのエネルギーを分子軌道のエネルギーで置き換えてイメージすれば良い。励起子バンドは HOMO-LUMO ギャップ内にできる。

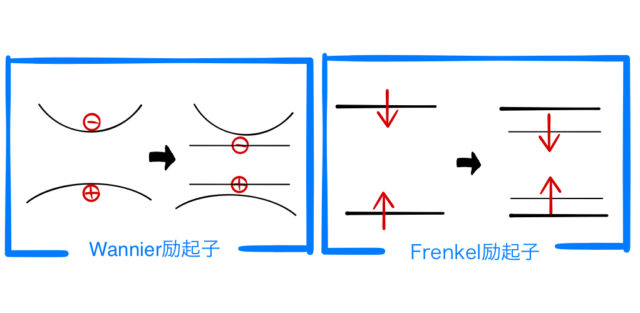
　図はWannier励起子とFrenkel励起子の状態である。矢印は励起された直後の左の状態から励起子を生成した時の様子を表している。

3. まとめ

　ここでは、Wannier励起子とFrenke励起子との違いの概要を述べた。

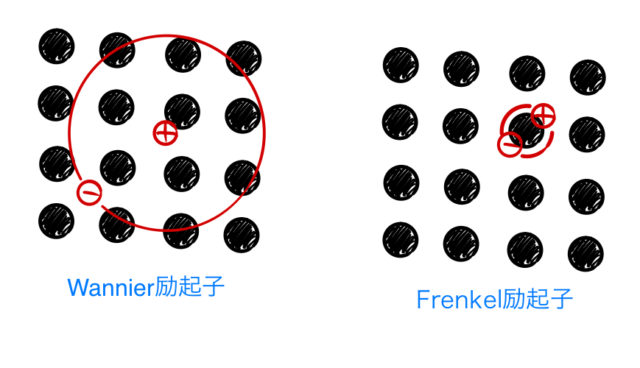
　非局在したWannier励起子と局在したFrenkel励起子をイメージとして持っておけば良い。Wannier励起子はざっくり言ってしまえば、正電荷と負電荷の結合である。したがって、励起子のエネルギーと半径を求めるためには水素原子モデルの類推を考えれば良い。

　より詳細については書籍等を参考にされたし。




コメントを残す

メールアドレスが公開されることはありません。