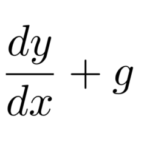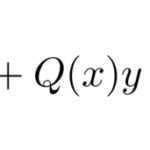高校数学では、3項間漸化式の問題は特性方程式を用いて解く(2章参照)。ここでは、別解として行列の対角化を用いた解法を紹介する。以下の例題を解いてみる。
以下の漸化式を満たす数列 ![]() の一般解を求めよ。
の一般解を求めよ。
![]()
1. 行列で漸化式を解く
1.1 行列で表現
例題の漸化式と等価な式を考える。以下のように考える。
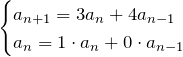
そうすると、この連立方程式は行列 ![]()
![]()
を用いて、
![]()
と表すことができる。
ここで、「一般項 ![]() を求める問題」は、「
を求める問題」は、「![]() を求める問題」に置き換わった。実際、漸化式を繰り返し使うと、
を求める問題」に置き換わった。実際、漸化式を繰り返し使うと、
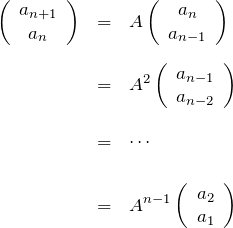
となる。結局、![]() が計算できれば
が計算できれば ![]() は求めることができる。以下では固有値と固有関数を用いて対角化した後に、
は求めることができる。以下では固有値と固有関数を用いて対角化した後に、![]() を計算する。
を計算する。
1.2 固有値・固有関数
![]() の固有値・固有関数を求めよう。
の固有値・固有関数を求めよう。![]() は2次の単位行列である。
は2次の単位行列である。
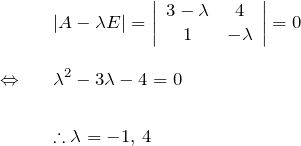
それぞれの固有値に対して、固有関数を求める。
(i) ![]() のとき:
のとき:
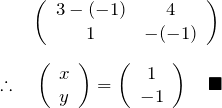
(ii) ![]() のとき:
のとき:
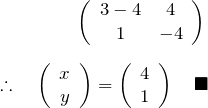
1.3 対角化/行列のn-1乗
上で求めた固有関数を使って対角化する。
![]()
と定義すると、![]() の逆行列は、
の逆行列は、
![]()
である。この ![]() と
と ![]() により
により ![]() を対角化する。(念の為計算して対角化されていることを確認した。)
を対角化する。(念の為計算して対角化されていることを確認した。)
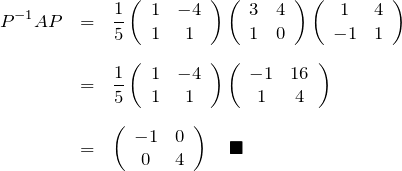
固有関数を並べた順番に、左上から固有値が並ぶように対角化される。最後の対角化行列を ![]() と置く。
と置く。
![]()
このとき、
![]() を求めるため、(*) 式の両辺を
を求めるため、(*) 式の両辺を ![]() 乗する。
乗する。
左辺:
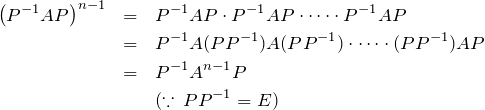
右辺:
![]()
これより ![]() が計算できる。
が計算できる。
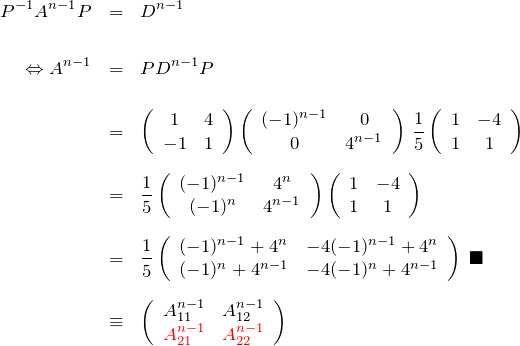
最終的に使うのは ![]() の要素のうち
の要素のうち ![]() と
と ![]() である。
である。
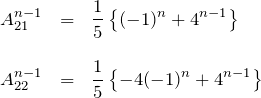
1.4 一般解
![]() がわかったので、
がわかったので、![]() と
と ![]() をつなげることができる。
をつなげることができる。
![]()
であるため、
![Rendered by QuickLaTeX.com \begin{eqnarray*} a_n &=& A^{n-1}_{11}a_2 + A^{n-1}_{11}a_1 \\ \\ &=& \frac{1}{5}\left[\quad\;(-1)^{n} + 4^{n-1}\right]a_2 \\ &+& \frac{1}{5}\left[ -4 (-1)^n + 4^{n-1}\right]a_1 \\ \\ &=& \frac{1}{5}\left\{(a_2-4a_1)\cdot(-1)^{n} + (a_2+a_1)\cdot4^{n-1}\right\} \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-02f63dfc4e1d2b9e5725041aace300ee_l3.png)
念の為、![]() を代入して正しいかどうか確認しておくのがよい。
を代入して正しいかどうか確認しておくのがよい。
2. 特性方程式で解く(高校数学レベル)
以下では、漸化式の特性方程式で解いた解法のうちの1つを示す。
【解答】
特性方程式は ![]() であるため、
であるため、
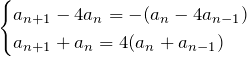
の2通りに変形できる。下の式を使う。これは公比4の等比数列であるため、
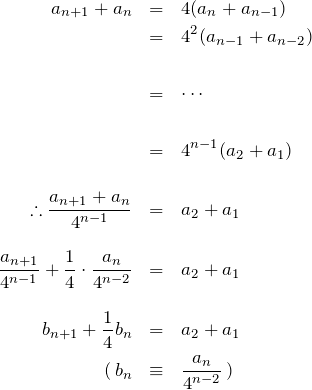
最後の行では、新たな数列 ![]() を定義した。
を定義した。![]() について以下のように変形する。
について以下のように変形する。
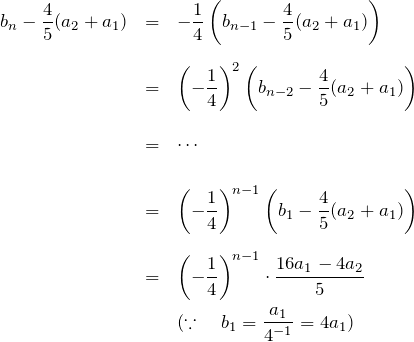
![]()
となる。![]() と直して、
と直して、
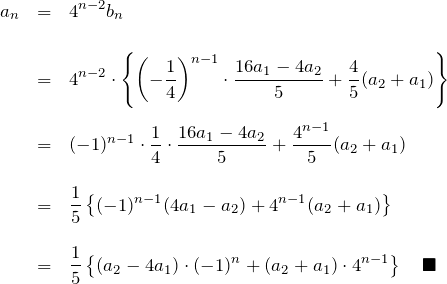
1.4 の最後にでてきた答えと一致する。どちらの方法が簡単かはわからない。
3. まとめ
行列の対角化を使って3項間漸化式を解いてきた。行列の固有値・固有関数を求めて対角化する練習問題にちょうどいい。