四重極モーメントについて学ぶ。双極モーメントについて理解されていることが望ましい。なぜなら、四重極モーメントは双極モーメントが0の場合に特に重要になるからである。
目次
1. 四重極モーメント
双極モーメントの繰り返しになるが、どのような状況のときに現れる項か知っておいた方が良い。双極モーメントは下図(右)のように電荷がある系から離れたところにおける、スカラーポテンシャルの第1近似であった。
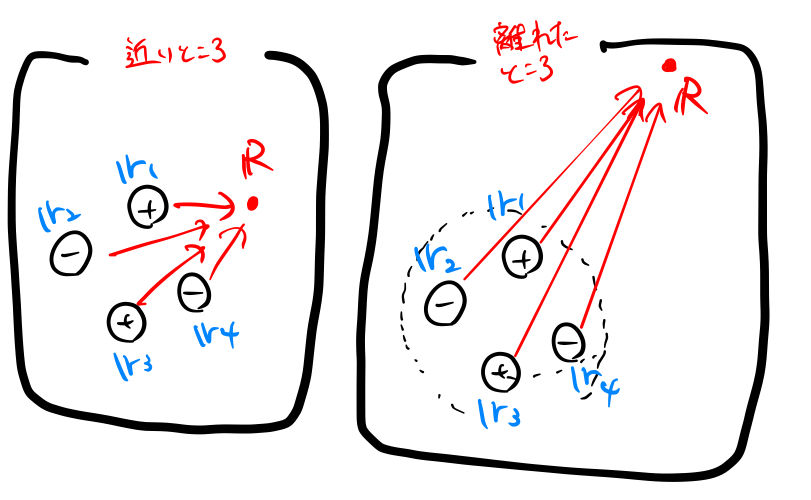
1.1 スカラーポテンシャルの多重極展開
座標原点を点線内に取ると、点線で囲んだ領域の電荷が ![]() につくるポテンシャルは、
につくるポテンシャルは、
![]()
と表すことができる。これを ![]() と仮定して展開して行った時の、2次の近似が四重極モーメントに対応するポンテシャルである。以下のように
と仮定して展開して行った時の、2次の近似が四重極モーメントに対応するポンテシャルである。以下のように ![]() で展開しよう(多重極展開)。
で展開しよう(多重極展開)。
![]()
![]() で展開したので
で展開したので ![]() は
は ![]() に比例する。双極モーメントに対応する
に比例する。双極モーメントに対応する ![]() は
は ![]() に比例する。四重極モーメントに対応する
に比例する。四重極モーメントに対応する ![]() (四重極ポテンシャル)は
(四重極ポテンシャル)は ![]() に比例する。
に比例する。
1.2 第一項
展開した時の第1項は ![]() であった。これは、点線の領域内の電荷の和
であった。これは、点線の領域内の電荷の和 ![]() を全電荷とする粒子を原点に置いて、その粒子が
を全電荷とする粒子を原点に置いて、その粒子が ![]() に作るポテンシャルに等しい。
に作るポテンシャルに等しい。
とにかく第0近似の ![]() では各電荷の位置を無視して、
では各電荷の位置を無視して、![]() へ作るポテンシャルを考える粗い近似である。実際、各電荷が原点からずれていれば各電荷の位置
へ作るポテンシャルを考える粗い近似である。実際、各電荷が原点からずれていれば各電荷の位置 ![]() に依存するが、遠くから見たら無視できるのである。
に依存するが、遠くから見たら無視できるのである。
1.3 第二項(双極モーメント)
第二項は、双極モーメント ![]() とすると、
とすると、
![]()
となる。grad が ![]() に作用するので、
に作用するので、![]() は
は ![]() に比例する。(分数関数の微分
に比例する。(分数関数の微分 ![]() と同様である。)
と同様である。)
これがモーメントと言われるゆえんは、![]() が原点からの距離と電荷(重み)の積になっているからである。
が原点からの距離と電荷(重み)の積になっているからである。
1.4 第三項(四重極モーメント)
このモーメントは前述した、![]() と
と ![]() が 0 のときに重要な項である。これらが
が 0 のときに重要な項である。これらが ![]() のときの条件は、
のときの条件は、
- 全電荷が0
- 双極モーメントが0
つまり、
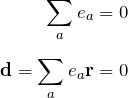
である。さて、![]() は
は ![]() の展開における2次の項であった。したがって、
の展開における2次の項であった。したがって、
![]()
となる。(2変数関数 ![]() のテイラー展開を思い出してほしい。)ここで、
のテイラー展開を思い出してほしい。)ここで、![]() は全電荷についてとり、小文字
は全電荷についてとり、小文字 ![]() などは点線の中の電荷の位置
などは点線の中の電荷の位置 ![]() の成分、大文字
の成分、大文字 ![]() などは
などは ![]() の成分を表す。
の成分を表す。
このポテンシャルには6個の量 ![]() が現れる。しかし、
が現れる。しかし、![]() はポアソン方程式を満たすため、つまり、
はポアソン方程式を満たすため、つまり、
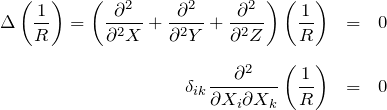
ここで最後の行ではクロネッカーのデルタを用いて ![]() ごとに偏微分することを明記した。このポアソン方程式のために、独立な変数は
ごとに偏微分することを明記した。このポアソン方程式のために、独立な変数は ![]() 個になる。この0となる項を適当な係数をつけて
個になる。この0となる項を適当な係数をつけて ![]() の中に入れ込むと、
の中に入れ込むと、
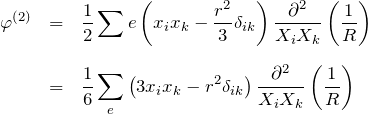
と書くことができる。この式に現れるテンソルを四重極モーメントという。
![]()
2. 四重極モーメントの性質
上で定義した四重極モーメントは、![]() の成分を持ったテンソル
の成分を持ったテンソル ![]() である。体格成分の和
である。体格成分の和 ![]() は 0になる。これは、ポアソン方程式を満たすところから来ている。また、先に述べたように、独立な成分は5つである。
は 0になる。これは、ポアソン方程式を満たすところから来ている。また、先に述べたように、独立な成分は5つである。
2.1 1/R を2階微分する
次に、![]() をみる。
をみる。![]() に注意して、まずは
に注意して、まずは ![]() で1階微分する。
で1階微分する。
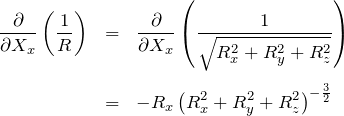
続いて、この結果をさらに ![]() で1階微分する。
で1階微分する。
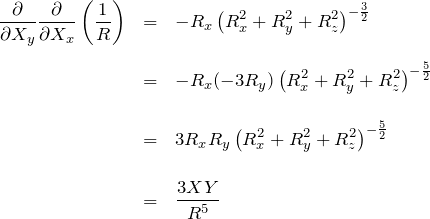
また、![]() について、
について、
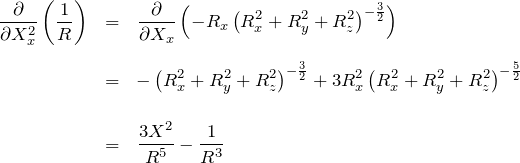
以上の結果をまとめると、
![]()
2.2 四重極モーメントで表すポテンシャル
上の結果から具体的に、ポテンシャル ![]() を求める。
を求める。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \varphi^{(2)} &=&\frac{D_{ik}}{6}\frac{\partial^2}{\partial X_i \partial X_k}\left(\frac{1}{R}\right) \\ \\ &=& \frac{D_{ik}}{6}\,\left[ \frac{3X_i X_k }{R^5} - \frac{\delta_{ik}}{R^3}\right] \\ \\ &=& \frac{D_{ik}X_i X_k}{2R^5} \quad (\because D_{ii}=0) \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-69cdfb49b6d0a1ef022ef06348e07661_l3.png)
このテンソル ![]() を対角化したときにでる3つの固有値のうち独立なものは2つである。なぜなら、
を対角化したときにでる3つの固有値のうち独立なものは2つである。なぜなら、![]() の対角要素の和 (
の対角要素の和 (![]() ) であるため、
) であるため、![]() の固有値
の固有値 ![]() となる。
となる。
3. まとめ
双極モーメントや四重極モーメントの導出は、ポテンシャルの展開により出てきたのであった。さらに高次の項も取ることが可能で、一般的にはこのような展開を多重極展開という。よく使うであろう、双極モーメント・四重極モーメントはおさえておきたい。