例題
また、この結果を用いて以下の無限級数の和を求めよ。
![]() で周期的な以下の関数
で周期的な以下の関数 ![]() をフーリエ級数に展開せよ。
をフーリエ級数に展開せよ。
![]()
また、この結果を用いて以下の無限級数の和を求めよ。
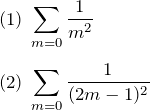
1. 解答
![]() のグラフは下のように周期的な
のグラフは下のように周期的な ![]() のグラフになる。
のグラフになる。
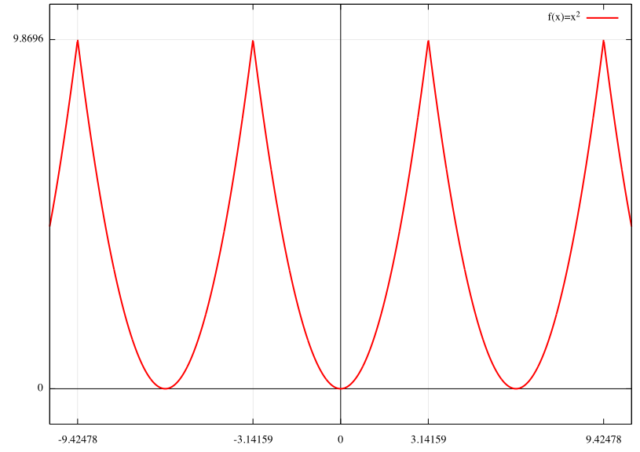
この関数は ![]() で偶関数である。
で偶関数である。
フーリエ級数展開
フーリエ級数で基本的に使うのは三角関数の直交性である。
三角関数の直交性
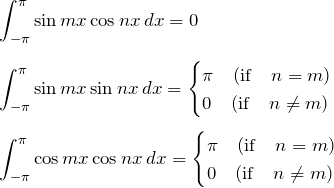
【解答】
周期関数 ![]() をフーリエ級数展開する。すなわち、周期
をフーリエ級数展開する。すなわち、周期 ![]() の三角関数シリーズで展開する。
の三角関数シリーズで展開する。
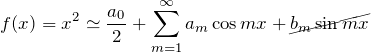
![]() が偶関数であるため、奇関数である
が偶関数であるため、奇関数である![]() のフーリエ係数 について
のフーリエ係数 について ![]() である。
である。
![]() について:
について:
![]() の両辺に
の両辺に ![]() をかけて、
をかけて、![]() で積分する。
で積分する。
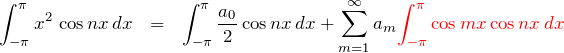
三角関数の直交性から、![]() の積分は
の積分は ![]() のとき
のとき ![]() で、
で、![]() のとき
のとき ![]() になる。したがって、
になる。したがって、
![]()
左辺の積分:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \int_{-\pi}^{\pi}x^2\,\cos nx \, dx &=& \int_{-\pi}^{\pi} x^2 \left(\frac{\sin nx}{n}\right)'\,dx\\\\ &=& \cancel{\left[x^2 \cdot \frac{\sin nx}{n}\right]_{-\pi}^{\pi}} -\frac{2}{n}\int_{-\pi}^{\pi} x\sin nx \, dx\\\\ &=& -\frac{2}{n}\left[ \frac{\sin nx}{n^2}-\frac{x\cos nx}{n} \right]_{-\pi}^{\pi}\\\\ &=& \frac{2}{n^2}\left\{ \pi \cos n\pi -(-\pi)\cos(-n\pi) \right\}\\\\ &=& \frac{4\pi}{n^2}\textcolor{red}{\cos n\pi}\\\\ &=& \frac{4\pi(-1)^n}{n^2}\quad\blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-d36d30c6688c555e8388eac8f21b9826_l3.png)
この計算にはフーリエ級数でよく使う下の関係を利用した。
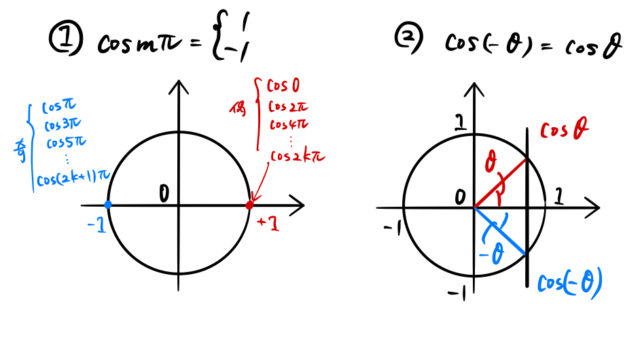
以上より、
![]()
![]() について、
について、![]() のフーリエ級数の式に
のフーリエ級数の式に ![]() をかけて
をかけて![]() で積分する。
で積分する。
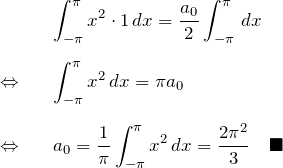
以上より、![]() をフーリエ級数に展開できる。
をフーリエ級数に展開できる。
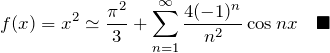
(1) の級数和
【解答】
![]()
を求めるために、![]() のフーリエ級数展開において、
のフーリエ級数展開において、![]() (連続点)とおく。
(連続点)とおく。
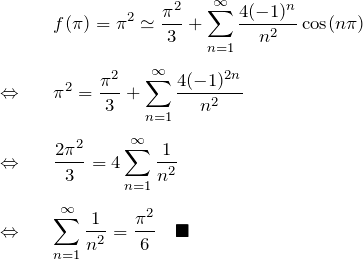
この結果はゼータ関数の1つとして知られている。
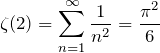
(2) の級数和
【解答】
(1)の結果から、
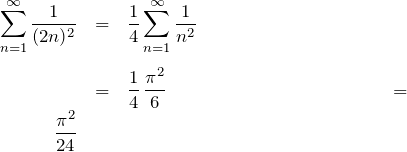
したがって、
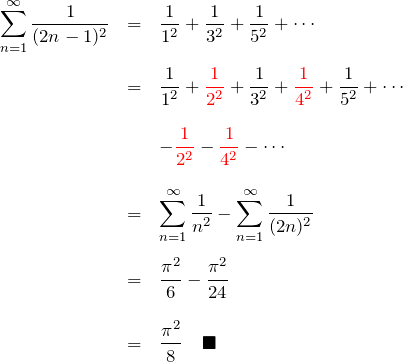
2. まとめ
よくある問題なので押さえておきたい。無限級数を求めるのもよくある問題である。
勉強させて頂きありがとうございます。
積分区間を-π→πから0→2πとして係数anを計算した場合、
anは4 / n^2となるという認識ですが、
積分区間を変えるとフーリエ級数和も変わるということなのでしょうか?
ご質問ありがとうございます。
もしかすると x^2 cos(nx) を0→2πで積分されているかもしれません。
今の場合 f(x)=x^2 となるのは [-π:π] の範囲のみで、[π:2π] の範囲ではf(x)=(x-2π)^2としてcos(nx)を乗じて積分すべきだと思います(初めのf(x)のグラフを参考にしてください。)。
要するに 0→2π の積分は、 x=π でf(x)の形が変わるので積分は分割しないといけないです。そうすると、積分区間を-π→πのanと一致します。
f(x)のフーリエ級数和(an,bnの値)は基本的には一意(1通り)に決まります。これは2次元ベクトルの座標を、xy直交座標系で表したときに成分が一通りに決まるのと同じ理屈です。フーリエ級数の場合、座標がan,bnの組に対応しています。x,yの基底に対応するものが、cos(nx),sin(nx)になっています。
* an=4/n^2 (>0)だと、cos(0)=1なので、an*cos(nx)の和であるf(x)についてf(x=0)は~0にならないです。本問題の答えの anについて、符号は(-1)^n になっています。したがって、プラスとマイナスを交互に足していくので f(x=0)~0 になります(答えのチェックになります)。