ミラー指数と逆格子ベクトル、面間隔、幾何学的関係
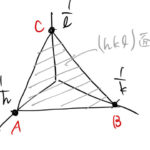
ミラー指数 の面と逆格子ベクトル などの幾何学。 これはほとんどベクトルの問題であるため、説明するための図が多くなっている。 前提知識 ミラー指数 以下の3点を通る平面を とする。 三次元空 …
もっと読む ミラー指数と逆格子ベクトル、面間隔、幾何学的関係バター猫のパラドックス

ミラー指数 の面と逆格子ベクトル などの幾何学。 これはほとんどベクトルの問題であるため、説明するための図が多くなっている。 前提知識 ミラー指数 以下の3点を通る平面を とする。 三次元空 …
もっと読む ミラー指数と逆格子ベクトル、面間隔、幾何学的関係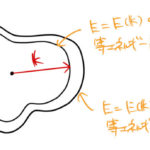
3次元の自由電子の状態密度は、 に比例する。 【参考】自由電子のフェルミ球、3次元の状態密度 自由電子でない場合の一般的な場合、3次元の状態密度は である。 は 番目のバンドを表す。係数の …
もっと読む 【固体物理】勾配∇で表す状態密度(導出)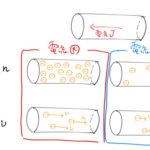
金属中の電流密度 は電子密度 、電荷 、電子の速度 によって与えることができる。ここでは以下の式を導出する。さらに電気伝導度、オームの法則について簡単にまとめる。 ポイント 1. 何が電流の …
もっと読む 金属中の電流密度 j=-nev /電気伝導度σ/オームの法則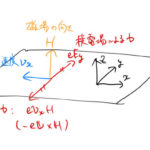
電流の流れている針金に電流に垂直な磁場をかければローレンツ力を受けることはよく知られている。ホール効果は針金中を運動する電子のレベルでのローレンツ力が重要な鍵になる。ここではそのホール効果の基礎を簡単にまとめよう。 1 …
もっと読む わかりやすいホール効果/ホール効果で分かること/ホール係数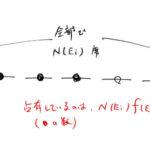
低温で、固体中の格子比熱は の振る舞いをすることがわかっているが、どうも実測値からずれてしまう。 その理由は、低温においては の振る舞いをする電子の比熱が重要であったからだ。 ここではその電子比熱の式を自由電子の状態密 …
もっと読む 自由電子の電子比熱/内部エネルギー/ゾンマーフェルト展開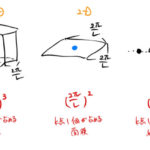
1次元(1D)、2次元(2D)、3次元(3D)の状態密度を下にまとめる。ここでは、以下の状態密度をすべて同じ考え方で求める方法を紹介する。3次元の計算に慣れている人は2章から。全くわからない場合は1章から。 状態密度ま …
もっと読む 1次元、2次元、3次元の状態密度まとめ(考え方と計算)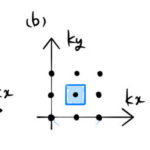
逆格子空間での は積分で置き換えた方が解析的に計算しやすいときがある。よく見る下の置き換えを証明して、わかりやすく説明する。 和を積分で置き換える 1. 適用条件 和を積分に置き換えて良い …
もっと読む 逆格子空間でのΣを積分 Ω/(2π)^3 ∫ で置き換える話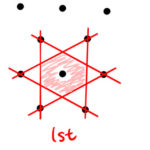
固体物理で非常に重要なブリルアンゾーン(Brillouin zone)の項目である。3次元のブリルアンゾーンを考える前に、2次元で考えておくと理解しやすい。簡単な定義と体積の求め方を2次元について説明する。 1. ブリ …
もっと読む 2次元のブリルアンゾーンの求め方/3次元ブリルアンゾーンの体積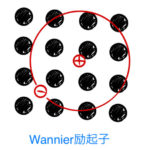
励起子(エキシトン;Exciton)は大きく分けてWannier励起子(ワニエ型)とFrenkel励起子(フレンケル型)の2種類ある。Wannier励起子は固体物理(特に無機物の半導体)において重要な励起状態である。一 …
もっと読む Wannier励起子とFrenkel励起子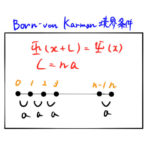
固体物理においては結晶を扱う。したがって、結晶格子は周期的に並んでいるという理想的な状態を考える。実際の結晶では有限的で表面があるために、なんとか表面を考えないようにしたい。こうして考え出されたのが、周期境界条件である …
もっと読む 周期境界条件(ボルン=フォン・カルマン境界条件)/波数kとは?